Cho tam giác ABC. Từ A vẽ một cung tròn có bán kính bằng BC và từ C vẽ một cung tròn có bán kính bằng AB, hai cung tròn này cắt nhau tại D (D nằm khác phía của B đối với AC). Kẻ AH vuông góc với BC (H thuộc BC) và CK vuông góc với AD (K thuộc AD). Chọn câu sai
Trả lời bởi giáo viên
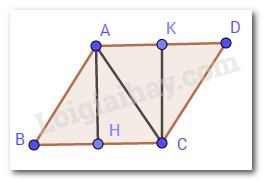
Xét \(\Delta ABC\) và \(\Delta CDA\) có:
\(\begin{array}{l}AC\;\;chung\\AB = CD\;(cmt)\\BC = DA\;(cmt)\\ \Rightarrow \Delta ABC = \Delta CDA(c - c - c)\end{array}\)
\( \Rightarrow \widehat {ACB} = \widehat {CAD}\) (hai góc tương ứng)
Mà 2 góc này ở vị trí so le trong nên AD // BC.
Ta có: \(\widehat {ACB} = \widehat {CAD}\;\;(cmt) \Rightarrow \widehat {ACH} = \widehat {CAK}\)
Xét \(\Delta AHC\) và \(\Delta CKA\) có:
\(\begin{array}{l}AC\;chung\\\widehat H = \widehat K = 90^\circ \;(gt)\\\widehat {ACH} = \widehat {CAK}\;\;\left( {cmt} \right)\end{array}\)
\( \Rightarrow \Delta AHC = \Delta CKA\) (cạnh huyền - góc nhọn)
\( \Rightarrow AH = CK\) ( hai cạnh tương ứng).
Do đó, A,B,D là các khẳng định đúng
Hướng dẫn giải:
+) Từ các trường hợp bằng nhau của tam giác vuông suy ra cặp cạnh tương ứng bằng nhau, các cặp góc tương ứng bằng nhau,
+) Sử dụng hai góc bằng nhau ở vị trí so le trong ta chứng minh được hai đường thẳng song song

