Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) nhọn nội tiếp \(\left( O \right)\). Hai đường cao \(BD\) và \(CE\) cắt nhau tại \(H\). Vẽ đường kính \(AF\) .
Hệ thức nào dưới đây là đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
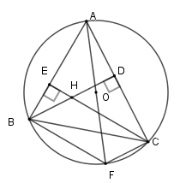
Xét hai tam giác vuông \(\Delta EBH\) và \(\Delta ECA\) có \(\widehat {EBH} = \widehat {ECA}\) (cùng phụ với \(\widehat {BAC}\) )
Nên $\Delta EBH\backsim\Delta ECA\left( {g - g} \right) $
$\Rightarrow \dfrac{{EB}}{{EC}} = \dfrac{{EH}}{{EA}} $
$\Rightarrow EB.EA = EC.EH$.
Hướng dẫn giải:
Sử dụng tam giác đồng dạng

