Câu hỏi:
2 năm trước
Cho tam giác $ABC$ có ba góc nhọn, đường cao $AH$ và nội tiếp đường tròn tâm $(O)$, đường kính $AM$
Gọi $N$ là giao điểm của $AH$ với đường tròn $(O)$. Tứ giác $BCMN$ là hình gì ?
Trả lời bởi giáo viên
Đáp án đúng: c
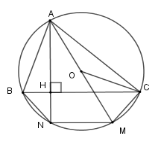
Xét \(\left( O \right)\) có \(\widehat {ANM}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ANM} = 90^\circ \) hay \(AN \bot NM\) mà \(BC \bot AN \Rightarrow NM{\rm{//}}BC\)
Lại có \(\widehat {BAN} = \widehat {CAM}\) (cmt)
nên cung $BN = $cung $CM$ \( \Rightarrow BN = CM\)
Từ đó tứ giác \(BNMC\) có \(NM{\rm{//}}BC\); \(BN = CM\) nên \(BNMC\) là hình thang cân.
Hướng dẫn giải:
+ Sử dụng hệ quả về góc nội tiếp và dấu hiệu nhận biết các hình đặc biệt:
+ Hình thang có hai cạnh bên bằng nhau là hình thang cân

