Cho phương trình $\dfrac{1}{2}\cos 4x + \dfrac{{4\tan x}}{{1 + {{\tan }^2}x}} = m$. Để phương trình vô nghiệm, các giá trị của tham số $m$phải thỏa mãn điều kiện
Trả lời bởi giáo viên
ĐK: $\cos x \ne 0.$
$\dfrac{1}{2}\cos 4x + \dfrac{{4\tan x}}{{1 + {{\tan }^2}x}} = m$$ \Leftrightarrow \dfrac{1}{2}\cos 4x + \dfrac{{4\tan x}}{{\dfrac{1}{{{{\cos }^2}x}}}} = m$$ \Leftrightarrow \dfrac{1}{2}\cos 4x + 4\sin x\cos x = m$
$ \Leftrightarrow \dfrac{1}{2}\left( {1 - 2{{\sin }^2}2x} \right) + 2\sin 2x = m$$ \Leftrightarrow {\sin ^2}2x - 2\sin 2x + m - \dfrac{1}{2} = 0$
Đặt $\sin 2x = t\,\left( {t \in \left[ { - 1;1} \right]} \right)$. Khi đó phương trình trở thành: ${t^2} - 2t + m - \dfrac{1}{2} = 0\,(*)$
Phương trình đã cho vô nghiệm \( \Leftrightarrow \left( * \right)\) không có nghiệm thuộc \(\left[ { - 1;1} \right]\).
Xét hàm \(f\left( t \right) = {t^2} - 2t\) có bảng biến thiên:
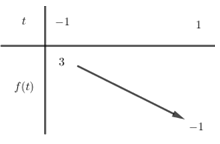
Từ bảng biến thiên ta thấy, phương trình \(\left( * \right)\) không có nghiệm thuộc \(\left[ { - 1;1} \right]\) nếu và chỉ nếu đường thẳng \(y = \dfrac{1}{2} - m\) không cắt đồ thị hàm số \(y = f\left( t \right)\) trong đoạn \(\left[ { - 1;1} \right]\)
\( \Leftrightarrow \left[ \begin{array}{l}\dfrac{1}{2} - m > 3\\\dfrac{1}{2} - m < - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < - \dfrac{5}{2}\\m > \dfrac{3}{2}\end{array} \right.\).
Hướng dẫn giải:
- Biến đổi phương trình về bậc hai ẩn \(\sin 2x\).
- Đặt \(t = \sin 2x\) và tìm điều kiện của \(t\).
- Tìm điều kiện để phương trình ẩn \(t\) không có nghiệm thỏa mãn điều kiện trên.

