Cho phản ứng hạt nhân \({}_0^1n + {}_3^6Li \to {}_1^3H + \alpha \). Hạt nhân \({}_3^6Li\) đứng yên, nơtron có động năng K_n = 2 MeV. Hạt α và hạt nhân \({}_1^3H\) bay ra theo các hướng hợp với hướng tới của nơtron những góc tương ứng bằng θ = 15⁰ và φ = 30⁰. Lấy tỉ số giữa các khối lượng hạt nhân bằng tỉ số giữa các số khối của chúng. Giả sử phản ứng không kèm theo bức xạ γ. Phản ứng tỏa hay thu bao nhiêu năng lượng?

Áp dụng đinh luật bảo toàn động lượng ta có: \(\overrightarrow {{P_n}}  + \overrightarrow {{P_{Li}}}  = \overrightarrow {{P_H}}  + \overrightarrow {{P_\alpha }} \)

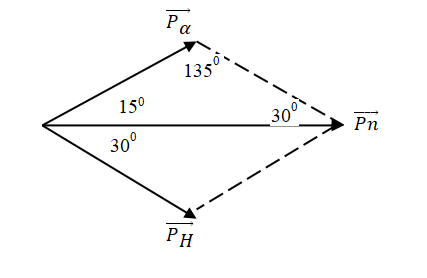
Ta có: P² = 2mK, K_n = 2 MeV

Áp dụng định lí hàm số sin trong tam giác ta được:  \(\frac{{{P_H}}}{{\sin 15}} = \frac{{{P_n}}}{{\sin 135}} = \frac{{{P_\alpha }}}{{\sin 30}}\)

\(\begin{array}{l} \Rightarrow {\left( {\frac{{{P_H}}}{{\sin 15}}} \right)^2} = {\left( {\frac{{{P_n}}}{{\sin 135}}} \right)^2} = {\left( {\frac{{{P_\alpha }}}{{\sin 30}}} \right)^2} \Leftrightarrow \frac{{3{K_H}}}{{{{\sin }^2}15}} = \frac{{1.{K_n}}}{{{{\sin }^2}135}} = \frac{{4{K_\alpha }}}{{{{\sin }^2}30}}\\ \Rightarrow {K_H} = 0,089MeV;{K_\alpha } = 0,25MeV\end{array}\)

∆E = K_α +  K_H  – Kn = - 1,66 MeV  < 0

=> Thu 1,66 MeV