Câu hỏi:
3 năm trước
Cho \((O)\), đường kính \(AB\), điểm \(D\) thuộc đường tròn. Gọi \(E\) là điểm đối xứng với \(A\) qua \(D.\)
Gọi \(K\) là giao điểm của \(EB\) với \((O)\). Chọn khẳng định sai?
Trả lời bởi giáo viên
Đáp án đúng: d
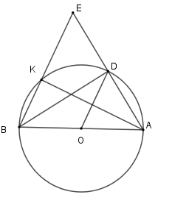
Xét \(\left( O \right)\) có $\widehat {BKA} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn) nên \(AK \bot BE\)
Mà \(OD\) là đường trung bình của tam giác \(ABE\) nên \(OD{\rm{//}}EB\) từ đó $OD \bot AK.$
Nên A, B, C đúng.
Hướng dẫn giải:
Sử dụng tính chất góc nội tiếp và quan hệ từ vuông góc đến song song

