Cho một mạch dao động LC lý tưởng, cuộn dây có độ tự cảm \(L = 4\mu H\). Tại thời điểm \(t{\rm{ }} = {\rm{ }}0\), dòng điện trong mạch có giá trị bằng một nửa giá trị cực đại của nó và có độ lớn đang tăng. Thời điểm gần nhất ( kể từ lúc \(t{\rm{ }} = {\rm{ }}0\)) để dòng điện trong mạch có giá trị bằng không là \(\dfrac{5}{6}{\rm{\mu s}}\). Điện dung của tụ điện là:
Trả lời bởi giáo viên
Biểu diễn trên đường tròn lượng giác:
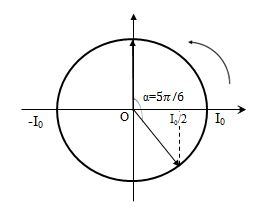
Ta thấy từ thời điểm t = 0 thời gian gần nhất để dòng điện trong mạch có giá trị bằng 0 là:
\(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{{5\pi }}{6}.\dfrac{T}{{2\pi }} = \dfrac{{5T}}{{12}} = \dfrac{5}{6} \Rightarrow T = 2\mu s \Rightarrow C = \dfrac{{{T^2}}}{{4{\pi ^2}L}} = 25nF\)
Hướng dẫn giải:
Sử dụng đường tròn lượng giác và công thức tính thời gian: \(\Delta t = \dfrac{{\Delta \varphi }}{\omega }\) (\(\Delta \varphi \) là góc quét được trong thời gian \(\Delta t\))