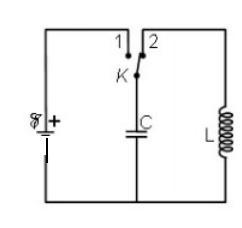
Cho mạch điện như hình vẽ. Biết $C = 500 pF$, $L = 0,2mH$, $E = 1,5 V$. Lấy $π^2= 10$. Tại thời điểm $t = 0$,  khóa K chuyển từ 1 sang 2. Thiết lập phương trình biểu diễn sự phụ thuộc của điện tích trên tụ điện C theo thời gian?

Một mạch dao động LC lí tưởng gồm cuộn cảm thuần có độ tự cảm 1H và tụ điện có điện dung \(10\mu F\). Lấy \({\pi ^2} = 10\). Lúc đầu điện tích trên tụ đạt giá trị cực đại. Điện tích trên tụ bằng 0 sau khoảng thời gian ngắn nhất là

Một mạch dao động lí tưởng có độ tự cảm \(L = 4\mu {\rm{H}}\) và điện dung \(C\). Tại thời điểm \(t\) thì cường độ dòng điện tức thời là \(2\;{\rm{mA}}\), tại thời điểm \(t + \frac{{\pi \sqrt {LC} }}{2}\) thì điện áp tức thời trên tụ điện là \(1\;{\rm{V}}\). Giá trị của \(C\) là

Trong mạch dao động lí tưởng có dao động điện từ tự do thì điện tích \(q\) trên mỗi bản tụ điện và cường độ dòng điện \(i\) trong cuộn cảm biến thiên điều hòa theo thời gian với:

Một tụ điện có điện dung \(10\mu F\) được tích điện đến một hiệu điện thế xác định. Sau đó nối hai bản tụ này vào một cuộn dây thuần cảm có độ tự cảm 1H. Bỏ qua điện trở của các dây nối, lấy \({\pi ^2} = 10\). Sau khoảng thời gian ngắn nhất là bao nhiêu (kể từ khi nối) điện tích trên tụ có giá trị bằng một nửa giá trị ban đầu?

Trong mạch dao động LC lí tưởng, cường độ dòng điện trong mạch dao động

Trong mạch dao động LC lí tưởng, điện áp trong mạch dao động

Dao động điện từ tự do trong mạch trong mạch LC có đường biểu diễn sự phụ thuộc của cường độ dòng điện qua cuộn dây theo thời gian như hình vẽ. Biểu thức điện tích tức thời trên tụ điện là