Cho lăng trụ tam giác đều \(ABC.{A^\prime }{B^\prime }{C^\prime }\) có cạnh đáy bằng \(a\) và \(A{B^\prime } \bot B{C^\prime }\). Tính thể tích của khối lăng trụ

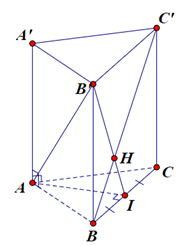
Gọi \(I\) là trung điềm $A B$. Vì \(ABC.{A^\prime }{B^\prime }{C^\prime }\) là lăng trụ tam giác đều nên. \(AI \bot \left( {B{B^\prime }{C^\prime }C} \right) = > AI \bot B{C^\prime }.\)

Lại có: \(A{C^\prime } \bot B{C^\prime }\) nên suy ra \(B{C^\prime } \bot \left( {AI{B^\prime }} \right) = > B{C^\prime } \bot {B^\prime }I\).

Gọi \(H = {B^\prime }I \cap B{C^\prime }\).

Ta có \(\Delta BHI\) đồng dạng \(\Delta {C^\prime }H{B^\prime } = > \dfrac{{HI}}{{{B^\prime }H}} = \dfrac{{BI}}{{{B^\prime }{C^\prime }}} = \dfrac{1}{2} = > {B^\prime }H = 2HI = > {B^\prime }I = 3HI\).

Xét tam giác vuông \({B^\prime }BI\) có:

\(B{I^2} = HI \cdot {B^\prime }I = 3H{I^2} = > HI = \sqrt {\dfrac{{B{I^2}}}{3}} = \sqrt {\dfrac{{{a^2}}}{{12}}} = \dfrac{{a\sqrt 3 }}{2}\).

Suy ra \(B{B^\prime } = \sqrt {{B^\prime }{I^2} - B{I^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt 2 }}{2}\)

Vậy \(V = {S_{\Delta ABC}}.B{B^\prime } = {{\rm{a}}^2}\dfrac{{\sqrt 3 }}{4} \cdot \dfrac{{a\sqrt 2 }}{2} = \dfrac{{{a^3}\sqrt 6 }}{8}\)