Cho lăng trụ đứng ABC.A’B’C’ có ABC là tam giác vuông \(AB = BC = 1;\,\,AA' = \sqrt 2 \), M là trung điểm của BC. Tính khoảng cách giữa 2 đường thẳng AM và B’C.

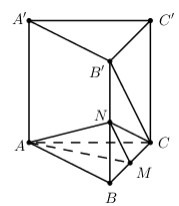
Gọi N là trung điểm của BB’ \( \Rightarrow MN//B'C\)

\( \Rightarrow \left( {AMN} \right)//B'C \Rightarrow d\left( {AM;B'C} \right) = d\left( {B'C;\left( {AMN} \right)} \right) = d\left( {C;\left( {AMN} \right)} \right)\).

Tam giác vuông ABC có \(AB = BC = 1 \Rightarrow \Delta ABC\) vuông cân tại B

\( \Rightarrow AM = \sqrt {A{B^2} + B{M^2}}  = \sqrt {1 + \dfrac{1}{4}}  = \dfrac{{\sqrt 5 }}{2}\)

Xét tam giác vuông BB’C có: \(B'C = \sqrt {BB{'^2} + B{C^2}}  = \sqrt {2 + 1}  = \sqrt 3  \Rightarrow MN = \dfrac{{\sqrt 3 }}{2}\)

Xét tam giác vuông ABN có: \(AN = \sqrt {A{B^2} + B{N^2}}  = \sqrt {{1^2} + {{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}}  = \dfrac{{\sqrt 6 }}{2}\).

\( \Rightarrow {S_{AMN}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}  = \dfrac{{\sqrt {14} }}{8}\)

Ta có: \({S_{AMC}} = \dfrac{1}{2}AB.MC = \dfrac{1}{2}.1.\dfrac{1}{2} = \dfrac{1}{4} \Rightarrow {V_{NAMC}} = \dfrac{1}{3}NM.{S_{AMC}} = \dfrac{1}{3}.\dfrac{{\sqrt 2 }}{2}.\dfrac{1}{4} = \dfrac{{\sqrt 2 }}{{24}}\).

Mà \({V_{N.AMC}} = \dfrac{1}{3}d\left( {C;\left( {AMN} \right)} \right).{S_{AMN}} \Rightarrow d\left( {C;\left( {AMN} \right)} \right) = \dfrac{{3{V_{NAMC}}}}{{{S_{AMN}}}} = \dfrac{{\dfrac{{\sqrt 2 }}{8}}}{{\dfrac{{\sqrt {14} }}{8}}} = \dfrac{{\sqrt 7 }}{7}\)