Cho khối chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\) và có thể tích \(V = \dfrac{{{a^3}\sqrt 3 }}{6}\). Tìm số \(r > 0\) sao cho tồn tại điểm \(J\) nằm trong khối chóp mà khoảng cách từ \(J\) đến các mặt bên và mặt đáy đều bằng \(r\)?

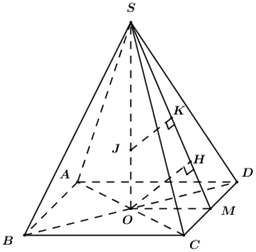
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\) .

Vì khoảng cách từ \(J\) đến các mặt bên và mặt đáy đều bằng \(r\) nên \(J \in SO\).

Gọi \(M\) là trung điểm của \(CD\), trong \(\left( {SOM} \right)\) kẻ \(OH \bot SM\) ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}CD \bot OM\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOM} \right) \Rightarrow CD \bot OH\\\left\{ \begin{array}{l}OH \bot CD\\OH \bot SM\end{array} \right. \Rightarrow OH \bot \left( {SCD} \right)\end{array}\)

Trong \(\left( {SOM} \right)\) kẻ \(JK\parallel OH \Rightarrow JK \bot \left( {SCD} \right) \Rightarrow d\left( {J;\left( {SCD} \right)} \right) = JK\).

Có \(d\left( {J;\left( {ABCD} \right)} \right) = JO\).

Theo bài ra ta có \(JK = JO = r\).

Ta có \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}\) \( \Rightarrow \dfrac{{{a^3}\sqrt 3 }}{6} = \dfrac{1}{3}SO.{a^2} \Rightarrow SO = \dfrac{{a\sqrt 3 }}{2}\).

Áp dụng hệ thức lượng trong tam giác vuông ta có: \(OH = \dfrac{{SO.OM}}{{\sqrt {S{O^2} + O{M^2}} }} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}.\dfrac{a}{2}}}{{\sqrt {\dfrac{{3{a^2}}}{4} + \dfrac{{{a^2}}}{4}} }} = \dfrac{{a\sqrt 3 }}{4}\).

Áp dụng định lí Ta-lét ta có

\(\begin{array}{l}\dfrac{{JK}}{{OH}} = \dfrac{{SJ}}{{SO}} \Rightarrow \dfrac{r}{{\dfrac{{a\sqrt 3 }}{4}}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2} - r}}{{\dfrac{{a\sqrt 3 }}{2}}}\\ \Leftrightarrow 2r = \dfrac{{a\sqrt 3 }}{2} - r\\ \Leftrightarrow 3r = \dfrac{{a\sqrt 3 }}{2} \Leftrightarrow r = \dfrac{{a\sqrt 3 }}{6}\end{array}\)