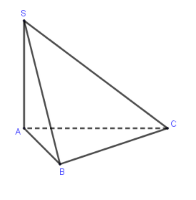
Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân tại \(A\), biết \(SA \bot \left( {ABC} \right)\), \(BC = 2a,\widehat {BAC} = {120^0}\), góc giữa mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng \({45^0}\). Tính thể tích khối chóp \(S.ABC\).
Trả lời bởi giáo viên
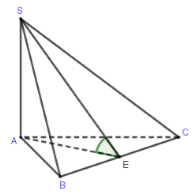
Gọi \(E\) là trung điểm của \(BC\) \( \Rightarrow \left\{ \begin{array}{l}AE \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAE} \right) \Rightarrow BC \bot SE\)
Ta có: \(\left\{ \begin{array}{l}AE \bot BC\\SE \bot BC\\\left( {ABC} \right) \cap \left( {SBC} \right) = BC\end{array} \right. \Rightarrow \angle \left( {\left( {ABC} \right);\left( {SBC} \right)} \right) = \angle SEA = {45^0}.\)
\( \Rightarrow \Delta SAE\) vuông cân tại \(A \Rightarrow SA = AE\).
Tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 2a\),
\(AE\) là tia phân giác của \(\widehat A\) \( \Rightarrow \widehat {BAE} = {60^0}\).
Tam giác vuông \(AEB\) có \(\widehat {BAE} = {60^0},BE = \dfrac{1}{2}BC = a \Rightarrow AE = \dfrac{{BE}}{{\tan {{60}^0}}} = \dfrac{{BE}}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{3} = SA\).
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.SA.\dfrac{1}{2}AE.BC = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{3}.\dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{3}.2a = \dfrac{{{a^3}}}{9}\).
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến.
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.

