Câu hỏi:
2 năm trước
Cho hình vuông \(ABCD\) cạnh bằng \(2\). Gọi \(M\) là trung điểm \(AB\). Cho tứ giác \(AMCD\) và các điểm trong của nó quay quanh trục \(AD\) ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
Trả lời bởi giáo viên
Đáp án đúng: c
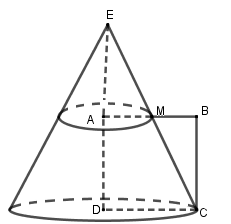
Kéo dài \(CM\) cắt \(DA\) tại \(E\). Quay hình thang vuông \(AMCD\) quanh trục \(AD\) ta được hình nón cụt như hình vẽ.
Quay tam giác \(EDC\) quanh trục \(ED\) ta được hình nón.
Dễ thấy \({V_{nc}} = {V_1} - {V_2}\), ở đó \({V_1}\) là thể tích khối nón đỉnh \(E\), bán kính đáy \(DC = 2\) và \({V_2}\) là thể tích khối nón đỉnh \(E\), bán kính đáy \(AM = 1\).
Có \(\dfrac{{EA}}{{ED}} = \dfrac{{AM}}{{DC}} = \dfrac{1}{2} \Rightarrow EA = AD = 2 \Rightarrow ED = 4\)
\( \Rightarrow {V_1} = \dfrac{1}{3}\pi D{C^2}.ED = \dfrac{1}{3}\pi {.2^2}.4 = \dfrac{{16\pi }}{3}\) ;
\({V_2} = \dfrac{1}{3}\pi A{M^2}EA = \dfrac{1}{3}\pi {.1^2}.2 = \dfrac{{2\pi }}{3}\).
Vậy \(V = {V_1} - {V_2} = \dfrac{{16\pi }}{3} - \dfrac{{2\pi }}{3} = \dfrac{{14\pi }}{3}\).
Hướng dẫn giải:
Vẽ thêm hình, sử dụng phương pháp cộng trừ thể tích các khối nón suy ra kết quả.
Chú ý: Công thức tính thể tích khối nón: \(V = \dfrac{1}{3}\pi {R^2}h\).
Câu hỏi khác
- Đề thi kiểm tra 1 tiết chương 6: Mặt nón, mặt trụ, mặt cầu - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 6: Mặt nón, trụ, cầu - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 6: Mặt nón, mặt trụ, mặt cầu - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 6: Mặt nón, trụ, cầu - Đề số 3 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 6: Mặt nón, trụ, cầu - Đề số 2 Toán 12 có lời giải chi tiết
