Câu hỏi:
2 năm trước
Cho hình vuông ABCD cạnh a, tại A và C đặt các điện tích q1 = q3 = q > 0. Cần đặt ở B điện tích bằng bao nhiêu để cường độ điện trường ở D bằng 0.
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có :
\(\left\{ \begin{array}{l}{E_1} = {E_3} = k\frac{{{q^2}}}{{{a^2}}}\\{E_{13}} = \sqrt {E_1^2 + E_3^2} = \sqrt 2 {E_1}\end{array} \right.\)
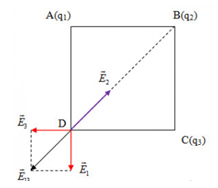
Để \({E_D} = 0 \to \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} = 0 \to \left\{ \begin{array}{l}\overrightarrow {{E_{13}}} \uparrow \downarrow \overrightarrow {{E_2}} \to {q_2} < 0\\{E_{13}} = {E_2}\end{array} \right.\)
\({E_2} = {E_{13}} \leftrightarrow {E_2} = \sqrt 2 {E_1} \leftrightarrow k\frac{{\left| {{q_2}} \right|}}{{{{\left( {a\sqrt 2 } \right)}^2}}} = k\frac{{\sqrt 2 \left| {{q_1}} \right|}}{{{{\left( a \right)}^2}}} \to \left| {{q_2}} \right| = 2\sqrt 2 \left| {{q_1}} \right| \to {q_2} = - 2\sqrt 2 q\)
Hướng dẫn giải:
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
