Trả lời bởi giáo viên
Đáp án đúng: a
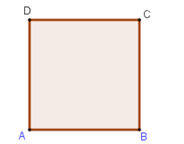
Ta có
S=|2→AD+→DB|=|→AD+→AD+→DB|=|→AD+→AB|=|→AC|=a√2.√2=2a.
Hướng dẫn giải:
- Sử dụng định nghĩa tích của một véc tơ với một số và quy tắc công véc tơ, quy tắc hình bình hành để tính véc tơ tổng 2→AD+→DB.
- Tính độ dài véc tơ vừa tìm được suy ra đáp án.
Chú ý: Hình vuông cạnh x thì độ dài đường chéo là x√2
Giải thích thêm:
Một số em có thể chọn nhầm đáp án D vì không để ý đề là hình vuông cạnh a√2 nên độ dài đường chéo AC=a√2.√2=2a chứ không phải AC=a√2

