Câu hỏi:
2 năm trước
Cho hình vẽ sau:
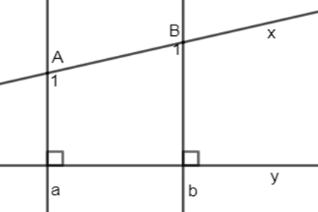
Biết \(a \bot y,\,b \bot y,\,\widehat {{A_1}} - \widehat {{B_1}} = {40^0}\). Tính \(\widehat {{B_1}}\).
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có: \(\left\{ \begin{array}{l}a \bot y\\b \bot y\end{array} \right.\left( {gt} \right) \Rightarrow a//\,b\) (quan hệ giữa tính vuông góc với tính song song)
\( \Rightarrow \widehat {{A_1}} + \widehat {{B_1}} = {180^0}\) (2 góc trong cùng phía bù nhau)
Lại có: \(\widehat {{A_1}} - \widehat {{B_1}} = {40^0}\left( {gt} \right) \Rightarrow \widehat {{B_1}} = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}\)
Hướng dẫn giải:
+ Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
+ Tính chất hai đường thẳng song song.