Cho hai đường thẳng $a$ và $b$ cùng vuông góc với đường thẳng $c,$ $c$ vuông góc với $a$ tại $M$ và vuông góc với $b$ tại $N.$ Một đường thẳng $m$ cắt $a,b$ tại $A,B.$ Biết \(\widehat {ABN} - \widehat {MAB} = 40^\circ \). Số đo góc $BAM$ là:
Trả lời bởi giáo viên
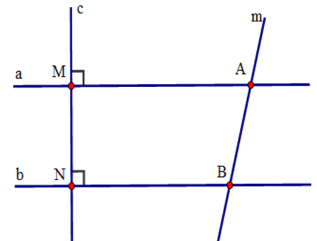
Từ đề bài ta có \(a \bot c;b \bot c \Rightarrow a//b\) (quan hệ từ vuông góc đến song song)
Suy ra \(\widehat {ABN} + \widehat {MAB} = 180^\circ \) (hai góc trong cùng phía bù nhau)
mà \(\widehat {ABN} - \widehat {MAB} = 40^\circ \)
nên \(\widehat {ABN} = \dfrac{{180^\circ + 40^\circ }}{2} = 110^\circ \) và \(\widehat {MAB} = 180^\circ - \widehat {ABN} \)\(= 180^\circ - 110^\circ = 70^\circ \)
Vậy \(\widehat {BAM} = 70^\circ .\)
Hướng dẫn giải:
+ Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
+ Tính chất hai đường thẳng song song.
+ Ta sử dụng cách tìm hai số khi biết tổng và hiệu như sau
\(x + y = a;x - y = b \Rightarrow x = \dfrac{{a + b}}{2};y = \dfrac{{a - b}}{2}\)