Trả lời bởi giáo viên
Đáp án đúng: b
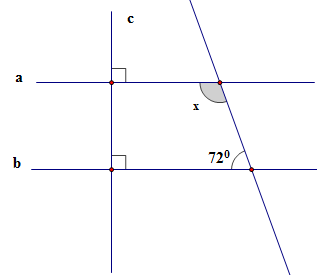
Từ hình vẽ ta có a⊥c;b⊥c⇒a//b (quan hệ từ vuông góc đến song song)
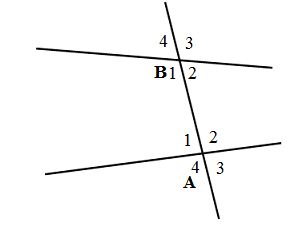
Ta có ^B1+^B2=180∘ (hai góc kề bù) suy ra ^B1=180∘−^B2=180∘−70∘=110∘
Vì a//b⇒^A2=^B1=110∘ (hai góc đồng vị bằng nhau)
Lại có ^A1=^A2=110∘ (hai góc đối đỉnh)
Vậy ^A1+^B1=110∘+110∘=220∘.
Hướng dẫn giải:
Sử dụng quan hệ từ vuông góc đến song song để suy ra a//b.
Sử dụng tính chất hai đường thẳng song song có hai góc trong cùng phía bù nhau.
Sử dụng hai góc đối đỉnh thì bằng nhau, hai góc kề bù có tổng số đo bằng 180∘.