Cho hình vẽ sau:
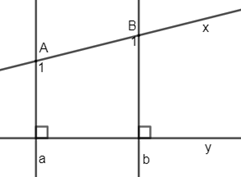
Biết \(a \bot y,\,b \bot y,\,\widehat {{A_1}} - \widehat {{B_1}} = {38^0}\). Tính \(\widehat {{B_1}}\).
Trả lời bởi giáo viên
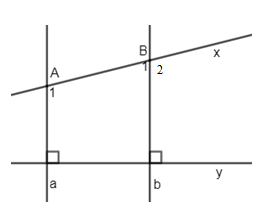
Vì a \( \bot \)y và b \( \bot \)y nên a // b (Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau).
\( \Rightarrow \widehat {{A_1}} = \widehat {{B_2}}\) ( 2 góc đồng vị)
Vì\(\,\widehat {{A_1}} - \widehat {{B_1}} = {38^0} \Rightarrow \widehat {{B_2}} - \widehat {{B_1}} = {38^0}\)
Mà \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù)
\( \Rightarrow \widehat {{B_1}} = \left( {180^\circ - 38^\circ } \right):2 = 71^\circ \)
Hướng dẫn giải:
+ Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
+ Áp dụng tính chất của 2 đường thẳng song song
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)