Câu hỏi:
2 năm trước
Cho hình vẽ như bên dưới:
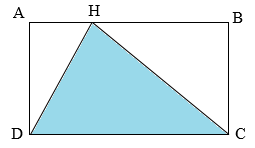
Tính diện tích hình tam giác \(HDC\). Biết hình chữ nhật \(ABCD\) có \(AB = 37cm,\,\,BC = 24cm\)
Trả lời bởi giáo viên
Đáp án đúng:
A. \(444c{m^2}\)
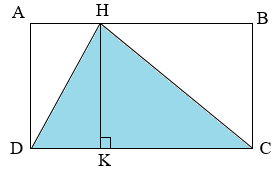
Kẻ \(HK\) vuông góc với \(CD\), khi đó \(HK\) là chiều cao tương ứng với cạnh đáy \(CD\).
Ta có chiều cao \(HK\) bằng chiều rộng của hình chữ nhật \(ABCD\) hay \(HK = BC = 24cm\)
Vì \(ABCD\) là hình chữ nhật nên \(CD = AB = 37cm\).
Diện tích tam giác \(HDC\) là:
\(37 \times 24:2 = 444\left( {c{m^2}} \right)\)
Đáp số: \(444c{m^2}\).
Hướng dẫn giải:
- Kẻ \(HK\) vuông góc với \(CD\), khi đó \(HK\) là chiều cao tương ứng với cạnh đáy \(CD\). Ta có chiều cao \(HK\) bằng chiều rộng của hình chữ nhật \(ABCD\): \(HK = BC = 24cm\).
- \(ABCD\) là hình chữ nhật nên \(CD = AB = 37cm\).
- Tính diện tích tam giác \(HCD\) theo công thức: \(S = a \times h:2\).
Trong một tam giác có:
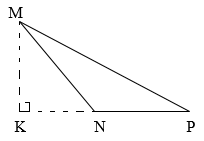
Độ dài cạnh đáy của hình tam giác có chiều cao \(24cm\) và diện tích là \(420c{m^2}\) là: 
Điền số thích hợp vào ô trống:
