Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AA’ = 2a, BC = a. Gọi M là trung điểm BB’. Bán kính mặt cầu ngoại tiếp khối chóp M.A’B’C’ bằng:

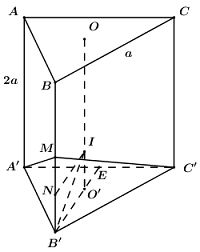
Gọi \(O,\,\,O'\) lần lượt là tâm tam giác đều ABC và A’B’C’, khi đó ta có OO’ là trục của (A’B’C’).

Gọi N là trung điểm của B’M, E là trung điểm của A’C’.

Qua N kẻ NI // B’E \(\left( {I \in OO'} \right)\) ta có:

\(\left\{ \begin{array}{l}B'E \bot BB'\\NI\parallel B'E\end{array} \right. \Rightarrow NI \bot BB'\) \( \Rightarrow IM = IB'\).

Lại có \(I \in OO'\) nên \(IA' = IB' = IC'\).

Do đó ta có \(IA' = IB' = IC' = IM\)  nên I là tâm mặt cầu ngoại tiếp chóp M.A’B’C’, bán kính \(R = IB'\).

Ta có: \(\left\{ \begin{array}{l}NI\parallel B'O'\\B'N\parallel O'I\end{array} \right.\) nên O’B’NI là hình bình hành \( \Rightarrow O'I = B'N = \dfrac{1}{2}B'M = \dfrac{1}{4}BB' = \dfrac{a}{2}\).

Tam giác A’B’C’ đều cạnh a nên \(B'E = \dfrac{{a\sqrt 3 }}{2} \Rightarrow B'O = \dfrac{2}{3}B'E = \dfrac{{a\sqrt 3 }}{3}\).

Áp dụng định lí Pytago trong tam giác vuông O’B’I có:

\(IB' = \sqrt {O'{I^2} + B'O{'^2}}  = \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{a\sqrt {21} }}{6}\).