Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác đều,  $M$ là trung điểm của $BC,$ ${\rm{AA}}' = AM = a$. Thể tích của lăng trụ bằng:

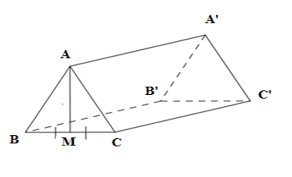
Vì tam giác $ABC$  là tam giác đều nên $AM$ vừa là trung tuyến vừa là đường cao của tam giác $ABC.$

Gọi chiều dài của cạnh tam giác $ABC$ là $x.\,\,\left( {x > 0} \right)$

\( \Rightarrow BM = MC = \dfrac{x}{2},\;AB = AC = BC = x\)

Xét tam giác vuông $MAC,$ ta có:

\(A{M^2} + M{C^2} = A{C^2} \Leftrightarrow {a^2} + \dfrac{{{x^2}}}{4} = {x^2} \Leftrightarrow \dfrac{{3{{\rm{x}}^2}}}{4} = {a^2} \Rightarrow x = \dfrac{{2\sqrt 3 }}{3}a\)

Vậy thể tích của hình lăng trụ là:

$V{\rm{ }} = {\rm{ }}{S_{ABC}}.h{\rm{ }} $ \(=\dfrac{1}{2}.AM.BC.AA' = \dfrac{1}{2}a.\dfrac{{2\sqrt 3 }}{3}a.a = \dfrac{{{a^3}\sqrt 3 }}{3}\)