Cho hình lăng trụ đứng ABC.A′B′C′ có AB=AC=BB′=a, \(\widehat {BAC} = {\rm{ }}{120^0}\). Gọi I là trung điểm của CC′. Cosin của góc tạo bởi hai mặt phẳng (ABC) và (AB′I) có dạng \(\dfrac{{\sqrt m }}{{10}}\). Tìm m.

Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b

Đáp án:

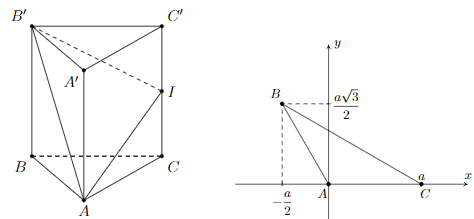
Gắn hệ trục tọa độ cho hình vẽ, sao cho \(A \equiv O\), C thuộc tia \(Ox\), A’ thuộc tia Oz và B thuộc góc phần tư thứ II của mặt phẳng Oxy

Ta có: \(A\left( {0;0;0} \right)\)

C thuộc tia \(Ox\) nên \(C\left( {a;0;0} \right)\)

=> \(C'\left( {a;0;a} \right)\)=>\(I\left( {a;0;\dfrac{a}{2}} \right)\)

\(\widehat {BAC} = {\rm{ }}{120^0}\) nên \(B\left( { - \dfrac{a}{2};\dfrac{{a\sqrt 3 }}{2};0} \right)\)

=> \(B'\left( { - \dfrac{a}{2};\dfrac{{a\sqrt 3 }}{2};a} \right)\)

\( \Rightarrow \overrightarrow {AB}  = \left( { - \dfrac{a}{2};\dfrac{{a\sqrt 3 }}{2};0} \right),\overrightarrow {AC}  = \left( {a;0;0} \right)\)

\( \Rightarrow \overrightarrow {{n_1}}  = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0;0; - \dfrac{{{a^2}\sqrt 3 }}{2}} \right)\)

\(\overrightarrow {AB'}  = \left( { - \dfrac{a}{2};\dfrac{{a\sqrt 3 }}{2};0} \right);\overrightarrow {AI}  = \left( {0;0; - \dfrac{{{a^2}\sqrt 3 }}{2}} \right)\)

\( \Rightarrow \overrightarrow {{n_2}}  = \left[ {\overrightarrow {AB'} ,\overrightarrow {AI} } \right] = \left( {\dfrac{{{a^2}\sqrt 3 }}{4};\dfrac{{5{a^2}}}{4}; - \dfrac{{{a^2}\sqrt 3 }}{2}} \right)\)

Gọi \(\alpha \)là góc giữa hai mặt phẳng (ABC) và (AB’I)

Khi đó:

\(\begin{array}{l}\cos \alpha  = \left| {\cos \left( {{n_1},{n_2}} \right)} \right| = \dfrac{{\left| {{n_1}.{n_2}} \right|}}{{\left| {{n_1}} \right|.\left| {{n_2}} \right|}} = \dfrac{{\sqrt {30} }}{{10}}\\ \Rightarrow m = 30\end{array}\)