Cho hình lăng trụ \(ABC.A'B'C'\) có thể tích bằng \(V\). Gọi \(M,\,\,N\) lần lượt là trung điểm của các cạnh \(AB,\,\,A'C'\). \(P\) là điểm trên cạnh \(BB'\) sao cho \(PB = 2PB'\). Tính \({V_{C.MNP}} =?\)

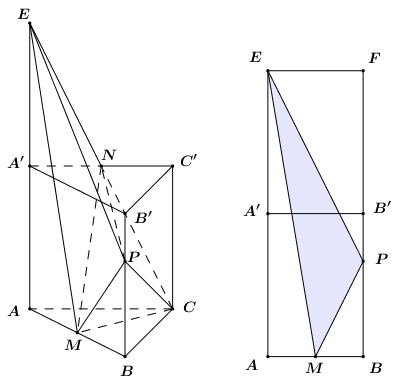
Không mất tính tổng quát, ta giả sử \(ABC.A'B'C'\) là lăng trụ đứng để bài toán đơn giản hơn.

Trong \(\left( {ACC'A'} \right)\) kéo dài \(NC\) cắt \(AA'\) tại \(E\).

Áp dụng định lí Ta-lét ta có \(\dfrac{{A'N}}{{AC}} = \dfrac{1}{2} = \dfrac{{EA'}}{{EA}} = \dfrac{{EN}}{{EC}}\) \( \Rightarrow N\) là trung điểm của của \(CE\) \( \Rightarrow \dfrac{{CN}}{{CE}} = \dfrac{1}{2}\).

Ta có: \(\dfrac{{{V_{C.MNP}}}}{{{V_{C.MEP}}}} = \dfrac{{CM}}{{CM}}.\dfrac{{CN}}{{CE}}.\dfrac{{CP}}{{CP}} = \dfrac{1}{2} \Rightarrow {V_{C.MNP}} = \dfrac{1}{2}{V_{C.MEP}}\).

Dựng hình chữ nhật \(ABFE\), ta có:

\({S_{ABFE}} = {S_{ABB'A'}}\); \(\dfrac{{{S_{EAM}}}}{{{S_{ABFE}}}} = \dfrac{1}{2}.\dfrac{{AM}}{{AB}} = \dfrac{1}{4}\); \(\dfrac{{{S_{PEF}}}}{{{S_{ABFE}}}} = \dfrac{1}{2}.\dfrac{{PF}}{{BF}} = \dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{3}\); \(\dfrac{{{S_{PMB}}}}{{{S_{ABFE}}}} = \dfrac{1}{2}.\dfrac{{PB}}{{BF}}.\dfrac{{BM}}{{AB}} = \dfrac{1}{2}.\dfrac{1}{3}.\dfrac{1}{2} = \dfrac{1}{{12}}\).

Khi đó ta có:

\(\begin{array}{l}{S_{MEP}} = {S_{ABFE}} - {S_{EAM}} - {S_{PEF}} - {S_{PMB}}\\\,\,\,\,\,\,\,\,\,\,\, = {S_{ABFE}} - \dfrac{1}{4}{S_{ABFE}} - \dfrac{1}{3}{S_{ABFE}} - \dfrac{1}{{12}}{S_{ABFE}}\\\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}{S_{ABFE}} = \dfrac{2}{3}{S_{ABB'A'}}\end{array}\)

Ta có: \(\dfrac{{{V_{C.MEP}}}}{{{V_{C.ABB'A'}}}} = \dfrac{{{S_{MEP}}}}{{{S_{ABB'A'}}}} = \dfrac{2}{3}\). Mà \({V_{C.ABB'A'}} = \dfrac{2}{3}V\) nên \({V_{C.MEP}} = \dfrac{2}{3}.\dfrac{2}{3}V = \dfrac{4}{9}V\).

Vậy \({V_{C.MNP}} = \dfrac{1}{2}{V_{C.MEP}} = \dfrac{2}{9}V\).