Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(B\) và \(A'A = A'B = A'C\). Biết rằng \(AB = 2a\), \(BC = \sqrt 3 a\) và mặt phẳng \(\left( {A'BC} \right)\) tạo với mặt phẳng đáy một góc \({45^0}\). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
Trả lời bởi giáo viên
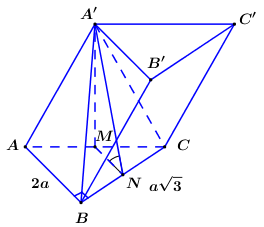
Gọi \(M,\,N\) lần lượt là trung điểm của \(AC,\,\,BC\).
Vì \(\Delta ABC\) vuông tại \(B\) nên \(M\) là tâm đường tròn ngoại tiếp \(\Delta ABC\), lại có \(A'A = A'B = A'C\) nên hình chiếu vuông góc của \(A'\) lên \(\left( {ABC} \right)\) trùng với tâm đường tròn ngoại tiếp \(\Delta ABC\) \( \Rightarrow A'M \bot \left( {ABC} \right)\).
Ta có \(MN\) là đường trung bình của \(\Delta ABC \Rightarrow MN//AB\) \( \Rightarrow MN \bot AC\) và \(MN = \dfrac{1}{2}AB = a\).
Ta có \(\left\{ \begin{array}{l}AC \bot MN\\AC \bot A'M\end{array} \right. \Rightarrow AC \bot \left( {A'MN} \right) \Rightarrow AC \bot A'N\).
\( \Rightarrow \angle \left( {\left( {A'BC} \right);\left( {ABC} \right)} \right) = \angle \left( {A'N;MN} \right) = \angle A'NM = {45^0}\).
\( \Rightarrow \Delta A'MN\) vuông cân tại \(M\) \( \Rightarrow A'M = MN = a\).
Vậy \({V_{ABC.A'B'C'}} = A'M.{S_{\Delta ABC}} = A'M.\dfrac{1}{2}AB.BC = a.\dfrac{1}{2}.2a.a\sqrt 3 = \sqrt 3 {a^3}\).
Hướng dẫn giải:
- Vì \(A'A = A'B = A'C\) nên hình chiếu vuông góc của \(A'\) lên \(\left( {ABC} \right)\) trùng với tâm đường tròn ngoại tiếp \(\Delta ABC\).
- Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông hoặc tính chất tam giác vuông cân tính chiều cao của lăng trụ.
- Thể tích khối lăng trụ có chiều cao \(h\), diện tích đáy \(B\) là \(V = Bh\).
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 3 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
