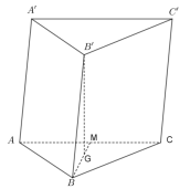
Cho hình lăng trụ \(ABC.A'B'C'\) có \(AA' = 2\sqrt {13} a\), tam giác \(ABC\) vuông tại \(C\) và \(\angle ABC = {30^0}\), góc giữa cạnh bên \(CC'\) và mặt đáy \(\left( {ABC} \right)\) bằng \({60^0}\). Hình chiếu vuông góc của \(B'\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trọng tâm của tam giác \(ABC\). Thể tích của khối tứ diện \(A'ABC\) theo \(a\) bằng:

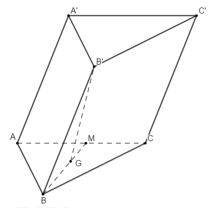
Ta có \(CC'//BB' \Rightarrow \angle \left( {CC';\left( {ABC} \right)} \right) = \angle \left( {BB';\left( {ABC} \right)} \right) = {60^0}\).

Vì \(B'G \bot \left( {ABC} \right)\) nên \(GB\) là hình chiếu vuông góc của \(B'B\) lên \(\left( {ABC} \right)\)

\( \Rightarrow \angle \left( {BB';\left( {ABC} \right)} \right) = \angle \left( {BB';BG} \right) = \angle B'BG = {60^0}\).

Xét tam giác vuông \(BB'G\) ta có: \(BB' = AA' = 2\sqrt {13} a\)

\( \Rightarrow B'G = BB'.\sin {60^0} = a\sqrt {39} \) và \(BG = BB'.\cos {60^0} = a\sqrt {13} \).

\( \Rightarrow BM = \dfrac{3}{2}BG = \dfrac{{3a\sqrt {13} }}{2}\).

Đặt \(BC = x \Rightarrow AC = BC.\tan {30^0} = \dfrac{{x\sqrt 3 }}{3} \Rightarrow MC = \dfrac{1}{2}AC = \dfrac{{x\sqrt 3 }}{6}\).

Áp dụng định lí Pytago trong tam giác vuông \(BMC\) ta có:

\(\begin{array}{l}B{M^2} = M{C^2} + B{C^2}\\ \Leftrightarrow {\left( {\dfrac{{3a\sqrt {13} }}{2}} \right)^2} = {\left( {\dfrac{{x\sqrt 3 }}{6}} \right)^2} + {x^2}\\ \Leftrightarrow \dfrac{{117{a^2}}}{4} = \dfrac{{13{x^2}}}{{12}}\\ \Leftrightarrow {x^2} = 27{a^2} \Rightarrow x = 3a\sqrt 3  = BC\\ \Rightarrow AC = 3a\end{array}\)

Nên \( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}.AC.BC = \dfrac{1}{2}.3a.3a\sqrt 3  = \dfrac{{9{a^2}\sqrt 3 }}{2}\).

Vậy \({V_{A'ABC}} = \dfrac{1}{3}.B'G.{S_{\Delta ABC}} = \dfrac{1}{3}.a\sqrt {39} .\dfrac{{9{a^2}\sqrt 3 }}{2} = \dfrac{{9{a^3}\sqrt {13} }}{2}\).