Câu hỏi:
2 năm trước
Cho hình hộp chữ nhật có kích thước như hình vẽ:
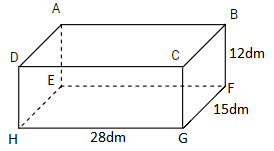
Tổng diện tích của mặt bên \(ADHE\) và mặt đáy \(ABCD\) là:
Trả lời bởi giáo viên
Đáp án đúng:
C. \(600d{m^2}\)
Vì hình đã cho là hình hộp chữ nhật nên ta có:
\(AD = HE = CB = GF = 15dm;\)
\(AB = CD = {\rm{EF = HG = 28dm;}}\)
\({\rm{DH = AE = CG = BF = 12dm}}\).
Diện tích mặt bên \(ADHE\) là:
\(12 \times 15 = 180\;(d{m^2})\)
Diện tích mặt đáy \(ABCD\) là:
\(28 \times 15 = 420\;(d{m^2})\)
Tổng diện tích của mặt bên \(ADHE\) và mặt đáy \(ABCD\) là:
\(180 + 420 = 600\;(d{m^2})\)
Đáp số: \(600d{m^2}\).
Hướng dẫn giải:
Vì hình đã cho là hình hộp chữ nhật nên ta có \(AD = HE = CB = GF = 15dm;\,\,AB = CD = {\rm{EF = HG = 28dm;}}\,\,{\rm{DH = AE = CG = BF = 12dm}}\)
Từ đó ta tìm được diện tích mặt bên \(ADHE\) và mặt đáy \(ABCD\), sau đó ta tìm được tổng diện tích hai mặt đó.
