Cho hình hộp \(ABCD.A'B'C'D'\) (tham khảo hình vẽ). Gọi \(M\) là trung điểm cạnh \(A'D'\) và \(\left( \alpha \right)\) là mặt phẳng đi qua \(M\), song song với các đường thẳng \(BB',AC.\) Gọi \(T\) là giao điểm của đường thẳng \(BC\) và mặt phẳng \(\left( \alpha \right)\). Tính tỉ số \(\dfrac{{TB}}{{TC}}.\)
Trả lời bởi giáo viên
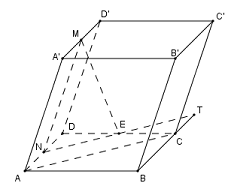
Gọi \(N,E\) lần lượt là trung điểm của \(AD,DC\)
Ta có \(MN//AA'//BB'\) và \(NE//AC\) (do \(NE\) là đường trung bình của tam giác \(DAC\))
Suy ra \(\left( \alpha \right) \equiv \left( {MNE} \right)\)
Trong \(\left( {ABCD} \right)\), kéo dài \(NE\) cắt \(BC\) tại \(T\). Suy ra \(ANTC\) là hình bình hành (do \(AN//TC;NT//AC\))
Do đó \(TC = AN = \dfrac{1}{2}AD = \dfrac{1}{2}BC\)
Ta có \(\left( {MNE} \right) \cap BC = \left\{ T \right\}\) nên \(\dfrac{{TB}}{{TC}} = \dfrac{{\dfrac{3}{2}BC}}{{\dfrac{1}{2}BC}} = 3\)
Hướng dẫn giải:
+ Dựng mặt phẳng \(\left( \alpha \right)\) dựa vào mối quan hệ song song với \(BB',AC\)
+ Từ đó tính tỉ số \(\dfrac{{TB}}{{TC}}\)


