Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, chiều cao của hình chóp bằng \(\dfrac{{a\sqrt 3 }}{2}\). Cosin góc giữa mặt bên và mặt đáy bằng
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
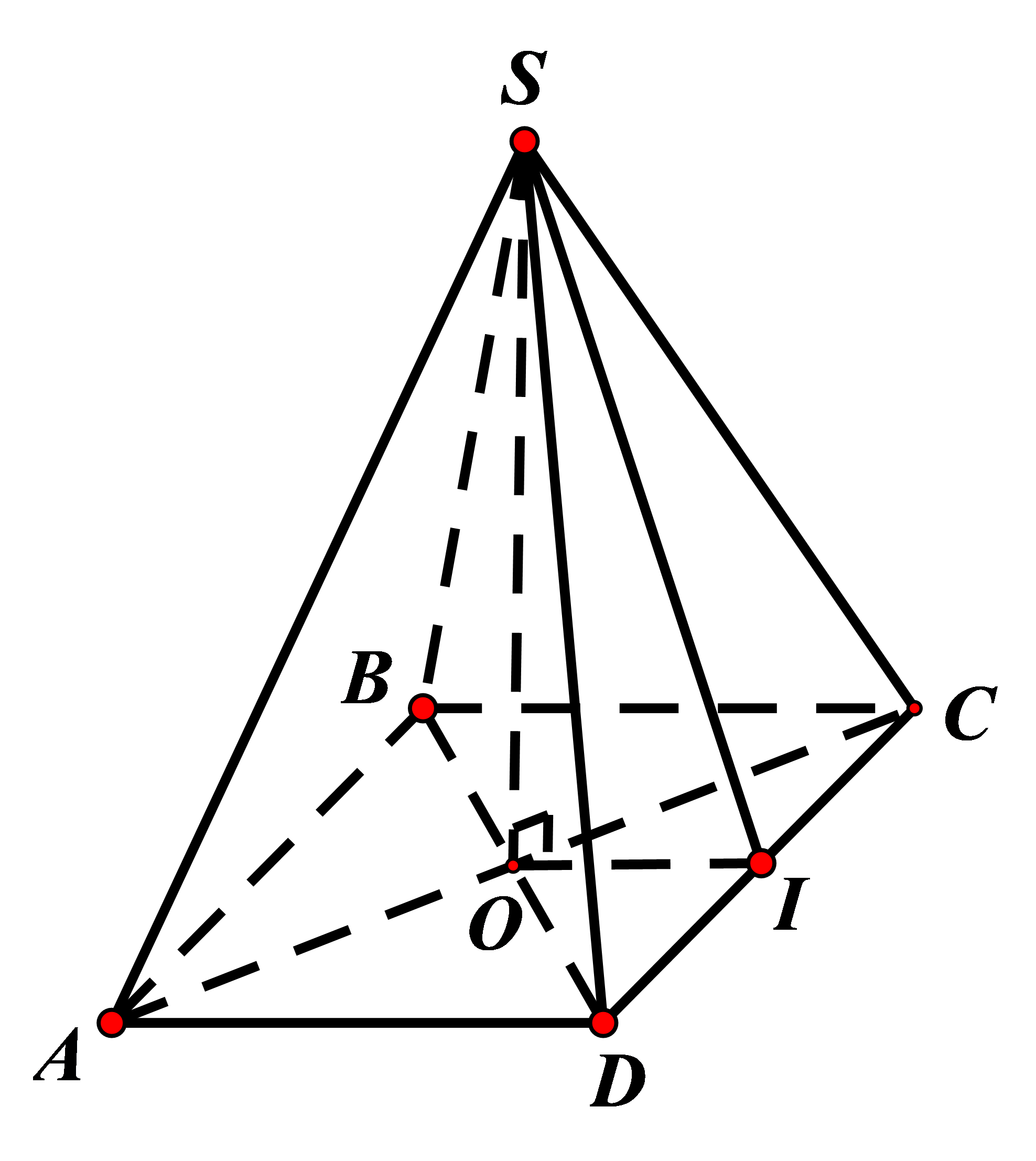
Gọi O là tâm của hình vuông ABCD, I là trung điểm của BC. Ta có:
\(\left\{ \begin{array}{l}BC \bot OI\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SOI} \right)\)
\(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SOI} \right) \bot BC\end{array} \right.\)\( \Rightarrow \widehat {\left( {\left( {SBC} \right),\left( {ABCD} \right)} \right)} = \widehat {\left( {SI,OI} \right)} = \widehat {SIO}\)
\(\Delta SOI\) vuông tại O
\(\begin{array}{l} \Rightarrow \tan \widehat {SOI} = \dfrac{{SO}}{{OI}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{{\dfrac{a}{2}}} = \sqrt 3 \\ \Rightarrow \widehat {SIO} = {60^0}\\ \Rightarrow \cos \widehat {SIO} = \dfrac{1}{2}\end{array}\)
Hướng dẫn giải:
- Gọi O là tâm của hình vuông ABCD, I là trung điểm của BC
- Xác dịnh góc giữa (SBC) và (ABCD)
- Tính góc.


