Cho hình chóp $S.ABCD$ có tất cả các cạnh đều bằng $\;a$. Gọi $I$ và $J$ lần lượt là trung điểm của $SC$ và $BC$. Số đo của góc $\left( {IJ,\;CD} \right)$ bằng:
Trả lời bởi giáo viên
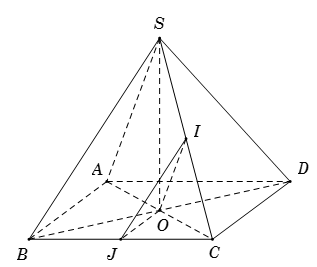
Gọi \(O\) là tâm của hình thoi \(ABCD \Rightarrow \)\(OJ\) là đường trung bình của \(\Delta BCD.\)
Suy ra \(\left\{ \begin{array}{l}OJ\,\parallel \,CD\\OJ = \dfrac{1}{2}CD\end{array} \right.\).
Vì \(CD\,\parallel \,OJ \Rightarrow \left( {IJ,CD} \right) = \left( {IJ,OJ} \right)\).
Xét tam giác $IOJ$, có \(\left\{ \begin{array}{l}IJ = \dfrac{1}{2}SB = \dfrac{a}{2}\\OJ = \dfrac{1}{2}CD = \dfrac{a}{2}\\IO = \dfrac{1}{2}SA = \dfrac{a}{2}\end{array} \right.\) $ \Rightarrow \Delta IOJ$ đều.
Vậy \(\left( {IJ,CD} \right) = \left( {IJ,OJ} \right) = \widehat {IJO} = 60^\circ \).
Hướng dẫn giải:
Dựa vào mối quan hệ song song và các kiến thức hình học đã biết để tính góc giữa \(IJ\) và \(CD\).

