Cho hình chóp S.ABCD có đáy là một hình vuông cạnh bằng a, cạnh SA=a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm của đoạn thẳng BC. Tính cosin của góc giữa (SMD) và mặt phẳng đáy.
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
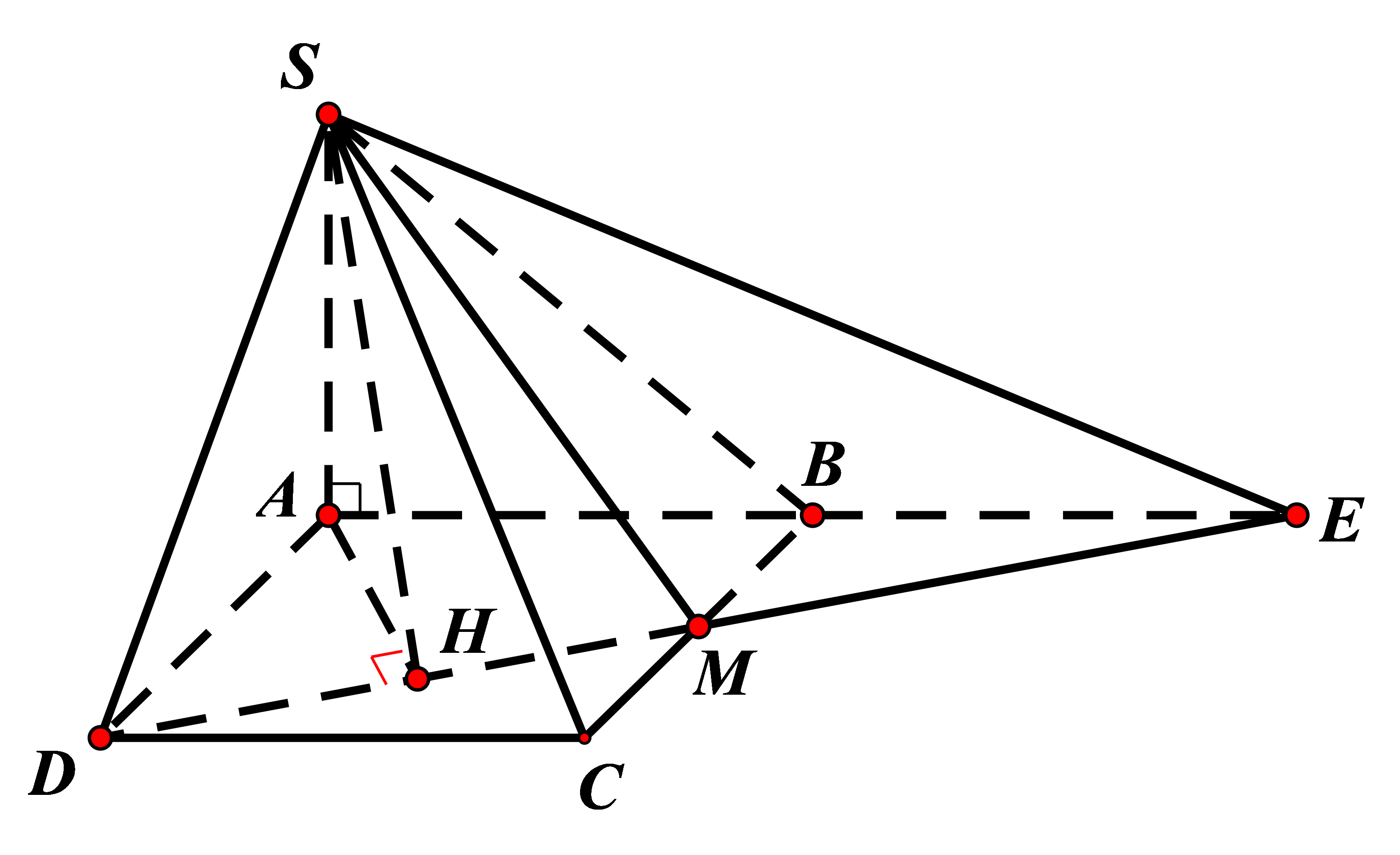
Kéo dài DM cắt AB tại điểm E.
Kẻ AH vuông góc với MD \(\left( {H \in DM} \right)\)
=> B là trung điểm của AE và góc giữa (SMD) và đáy là \(\widehat {SHA}\)
Xét tam giác ADE vuông tại A có đường cao AH, ta có:
\(AH = \dfrac{{AD.AE}}{{DE}} = \dfrac{{AD.AE}}{{\sqrt {A{D^2} + A{E^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}\)
\(\tan \widehat {SHA} = \dfrac{{SA}}{{HA}} = \dfrac{{\sqrt 5 }}{2}\)
\( \Rightarrow \cos \widehat {SHA} = \sqrt {\dfrac{1}{{1 + {{\tan }^2}\widehat {SHA}}}} = \dfrac{2}{3}\)
Hướng dẫn giải:
- Kéo dài DM cắt AB tại điểm E. Kẻ AH vuông góc với MD \(\left( {H \in DM} \right)\)
- Xác định góc góc giữa (SMD) và đáy
- Sử dụng hệ thức lượng để tính góc.
- Sử dụng công thức \({\tan ^2}x + 1 = \dfrac{1}{{{{\cos }^2}x}}\)
Câu hỏi khác
(Nguồn: ourwordindata.org)- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
