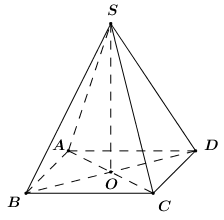
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\), cạnh \(a\). Đường thẳng \(SO\) vuông góc với mặt phẳng đáy và \(SO = \dfrac{{a\sqrt 3 }}{2}\). Tính góc giữa \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\).

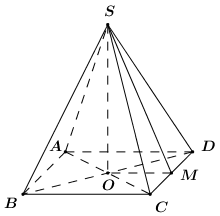
Gọi \(M\) là trung điểm của \(CD\) ta có \(OM\) là đường trung bình của tam giác \(ACD\) nên \(OM\parallel AD \Rightarrow OM \bot CD\) và \(OM = \dfrac{1}{2}AD = \dfrac{a}{2}\).

Ta có: \(\left\{ \begin{array}{l}CD \bot OM\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOM} \right) \Rightarrow CD \bot SM\).

\(\left\{ \begin{array}{l}\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\\left( {SCD} \right) \supset SM \bot CD\\\left( {ABCD} \right) \supset OM \bot CD\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle \left( {SM;OM} \right) = \angle SMO\).

Xét \(\Delta SOM\) vuông tại \(O\) có: \(\tan \angle SMO = \dfrac{{SO}}{{OM}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{{\dfrac{a}{2}}} = \sqrt 3 \) \( \Rightarrow \angle SMO = {60^0}\).

Vậy \(\angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = {60^0}\).