Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $D$, đáy lớn $AB$; cạnh bên $SA$ vuông góc với đáy. Gọi $Q$ là điểm trên cạnh $SA$ và $Q \ne A,$ $Q \ne S$; $M$ là điểm trên đoạn $AD$ và $M \ne A$. Mặt phẳng $\left( \alpha \right)$ qua $QM$ và vuông góc với mặt phẳng $\left( {SAD} \right)$. Thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp đã cho là:
Trả lời bởi giáo viên
Đáp án đúng: c
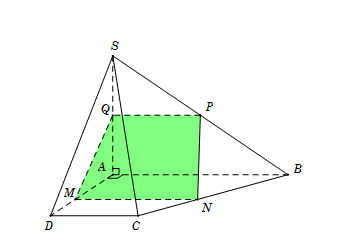
Ta có $\left\{ \begin{array}{l}AB \bot AD\\AB \bot SA\end{array} \right. \Rightarrow AB \bot \left( {SAD} \right)$. Mà $\left( \alpha \right) \bot \left( {SAD} \right)$ suy ra $AB\parallel \left( \alpha \right)$.
Qua $M$ kẻ đường thẳng song song với $AB$ cắt $BC$ tại $N$.
Qua $Q$ kẻ đường thẳng song song với $AB$ cắt $SB$ tại $P$.
Khi đó thiết diện là hình thang $MNPQ$ (do \(MN\parallel PQ\)).
Vì $AB \bot \left( {SAD} \right)$ suy ra $MN \bot \left( {SAD} \right)$ nên $MN \bot MQ$.
Do đó thiết diện $MNPQ$ là hình thang vuông tại Q và $M$.
