Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $D$, $AB = 2a,{\rm{ }}AD = DC = a$; cạnh bên $SA = a$ và vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ qua $SD$ và vuông góc với mặt phẳng $\left( {SAC} \right)$. Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp đã cho.
Trả lời bởi giáo viên
Đáp án đúng: c
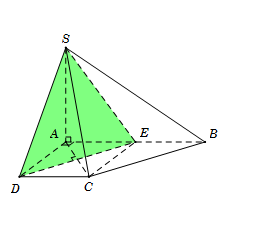
Gọi $E$ là trung điểm $AB$.
Suy ra $AECD$ là hình vuông nên $DE \bot AC$. $\left( 1 \right)$
Mặt khác $SA \bot \left( {ABCD} \right) \Rightarrow SA \bot DE$. $\left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$, suy ra $DE \bot \left( {SAC} \right) \Rightarrow \left( {SDE} \right) \bot \left( {SAC} \right)$.
Ta có $\left. \begin{array}{l}\left( {SDE} \right) \supset SD\\\left( {SDE} \right) \bot \left( {SAC} \right)\end{array} \right\} \Rightarrow \left( \alpha \right) \equiv \left( {SDE} \right).$
Vậy thiết diện là tam giác $SDE$
Ta có $SD = \sqrt {S{A^2} + D{A^2}} = a\sqrt 2 ;{\rm{ }}SE = \sqrt {S{A^2} + A{E^2}} = a\sqrt 2 $; $DE = AC = DC\sqrt 2 = a\sqrt 2 $.
Do đó tam giác $SDE$ đều có cạnh $a\sqrt 2 $ nên ${S_{\Delta \,SDE}} = \dfrac{{S{D^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{2}$.
