Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật tâm $O$ với $AB = a,$ $AD = 2a.$ Cạnh bên $SA = a$ và vuông góc với đáy. Gọi $\left( \alpha \right)$ là mặt phẳng qua $SO$ và vuông góc với $\left( {SAD} \right).$ Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ và hình chóp đã cho.
Trả lời bởi giáo viên
Đáp án đúng: b
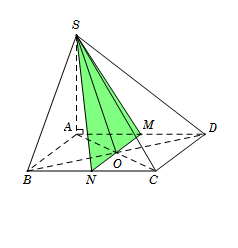
Gọi $M,{\rm{ }}N$ lần lượt là trung điểm $AD,{\rm{ }}BC$. Khi đó
\( \bullet \) $MN$ đi qua $O.$
\( \bullet \) $\left\{ \begin{array}{l}MN \bot AD\\MN \bot SA\end{array} \right. \Rightarrow MN \bot \left( {SAD} \right).$
Từ đó suy ra $\left( \alpha \right) \equiv \left( {SMN} \right)$ và thiết diện cần tìm là tam giác $SMN$.
Tam giác $SMN$ vuông tại $M$ nên
${S_{\Delta \,SMN}} = \dfrac{1}{2}SM.MN = \dfrac{1}{2}\sqrt {S{A^2} + {{\left( {\dfrac{{AD}}{2}} \right)}^2}} .AB = \dfrac{{{a^2}\sqrt 2 }}{2}.$
