Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I,{\rm{ }}J\) lần lượt là trung điểm \(SA,{\rm{ }}SB.\) Khẳng định nào sau đây sai?
Trả lời bởi giáo viên
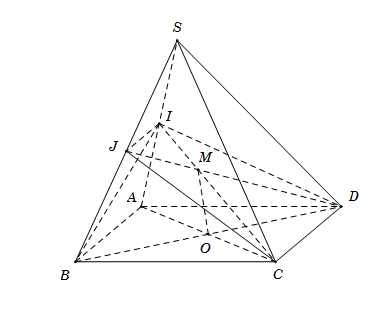
\( \bullet \) Ta có \(IJ\) là đường trung bình của tam giác \(SAB\) \( \Rightarrow IJ\parallel AB\parallel CD \Rightarrow IJ\parallel CD\)
\( \Rightarrow IJCD\) là hình thang. Do đó A đúng.
\( \bullet \) Ta có \(\left\{ \begin{array}{l}IB \subset \left( {SAB} \right)\\IB \subset \left( {IBC} \right)\end{array} \right. \Rightarrow \left( {SAB} \right) \cap \left( {IBC} \right) = IB.\) Do đó B đúng.
\( \bullet \) Ta có \(\left\{ \begin{array}{l}JD \subset \left( {SBD} \right)\\JD \subset \left( {JBD} \right)\end{array} \right. \Rightarrow \left( {SBD} \right) \cap \left( {JBD} \right) = JD.\) Do đó C đúng.
\( \bullet \) Trong mặt phẳng \(\left( {IJCD} \right)\), gọi \(M = IC \cap JD\)$ \Rightarrow \left( {IAC} \right) \cap \left( {JBD} \right) = MO.$ Do đó D sai.
Hướng dẫn giải:
- Xét tính đúng sai của các đáp án bằng cách tìm giao tuyến của mỗi cặp mặt phẳng đã cho ở mỗi đáp án.

