Cho điểm $A$ không nằm trên mặt phẳng $\left( \alpha \right)$ chứa tam giác $BCD.$ Lấy $E,\,\,F$ là các điểm lần lượt nằm trên các cạnh $AB,\,\,AC.$ Khi $EF$ và $BC$ cắt nhau tại $I,$ thì $I$ không phải là điểm chung của hai mặt phẳng nào sau đây?
Trả lời bởi giáo viên
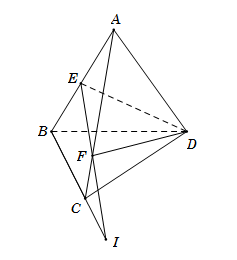
Điểm $I$ là giao điểm của $EF$ và $BC$ mà
\(\left\{ \begin{array}{l}BC \subset \left( {BCD} \right)\\EF \subset \left( {DEF} \right)\\EF \subset \left( {ABC} \right)\\EF \subset \left( {AEF} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}I \in \left( {BCD} \right) \cap \left( {DEF} \right)\\I \in \left( {BCD} \right) \cap \left( {ABC} \right)\\I \in \left( {BCD} \right) \cap \left( {AEF} \right)\end{array} \right.\)
Hướng dẫn giải:
Xác định các đường thẳng $EF,BC$ nằm trong mặt phẳng nào, từ đó suy ra điểm \(I\) nằm trong mặt phẳng nào.

