Câu hỏi:
2 năm trước
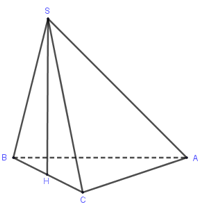
Cho hình chóp \(S.ABC\) đáy \(ABC\) là tam giác vuông tại \(A,AB = a,AC = a\sqrt 3 \). Tam giác $SBC$ đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp $S.ABC$
Trả lời bởi giáo viên
Đáp án đúng: a
Trong $mp(SBC)$ kẻ \(SH \bot BC\left( {H \in BC} \right) \Rightarrow SH \bot \left( {ABC} \right),H\) là trung điểm \(BC\)
Xét tam giác vuông $ABC$ có \(BC = \sqrt {{a^2} + 3{a^2}} = 2a \Rightarrow \Delta SBC\) đều cạnh $2a$
\( \Rightarrow SH = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}} = \dfrac{1}{6}SH.AB.AC = \dfrac{1}{2}{a^3}\)
Hướng dẫn giải:
Bước 1: Xác định chiều cao hình chóp
Bước 2: Áp dụng công thức tính thể tích hình chóp
Câu hỏi khác
- Đề thi kiểm tra 15 phút chương 5: Khối đa diện và thể tích - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 5: Khối đa diện và thể tích - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 5: Khối đa diện và thể tích - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 5: Khối đa diện và thể tích - Đề số 3 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 5: Khối đa diện và thể tích - Đề số 3 Toán 12 có lời giải chi tiết
