Cho hình chóp đều $S.ABCD$ có diện tích đáy là $16c{m^2}$, diện tích một mặt bên là $8\sqrt 3 c{m^2}$. Thể tích khối chóp $S.ABCD$ là:

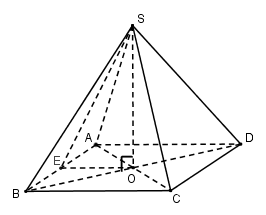
Gọi $O = AC \cap BD$. Vì chóp $S.ABCD$ đều nên $SO \bot \left( {ABCD} \right)$

Vì chóp $S.ABCD$ đều nên $ABCD$ là hình vuông $\Rightarrow {S_{ABCD}} = A{B^2} = 16 \Rightarrow AB = 4\left( {cm} \right) = AD$

Gọi $E$ là trung điểm của AB$\Rightarrow OE$ là đường trung bình của tam giác ABD$\Rightarrow OE//AD \Rightarrow OE \bot AB$ và $OE = \dfrac{1}{2}AD = \dfrac{1}{2}.4 = 2\left( {cm} \right)$

$\left. \begin{array}{l}OE \bot AB\\SO \bot AB\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow AB \bot \left( {SOE} \right) \Rightarrow AB \bot SE$

$\Rightarrow {S_{\Delta SAB}} = \dfrac{1}{2}SE.AB = 8\sqrt 3  \Rightarrow SE = \dfrac{{16\sqrt 3 }}{{AB}} = \dfrac{{16\sqrt 3 }}{4} = 4\sqrt 3 \left( {cm} \right)$

$SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OE \Rightarrow \Delta SOE$ vuông tại O$\Rightarrow SO = \sqrt {S{E^2} - O{E^2}}  = \sqrt {48 - 4}  = \sqrt {44}  = 2\sqrt {11} \left( {cm} \right)$

Vậy ${V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.2\sqrt {11} .16 = \dfrac{{32\sqrt {11} }}{3}\left( {c{m^3}} \right)$