Cho hình chóp S.ABC có SA vuông góc với đáy, SA=2BC=2a và \(\widehat {BAC} = {120^0}\). Gọi M và N lần lượt là hình chiếu của A lên đoạn SB, SC. Tính cosin góc giữa (AMN) và đáy.
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
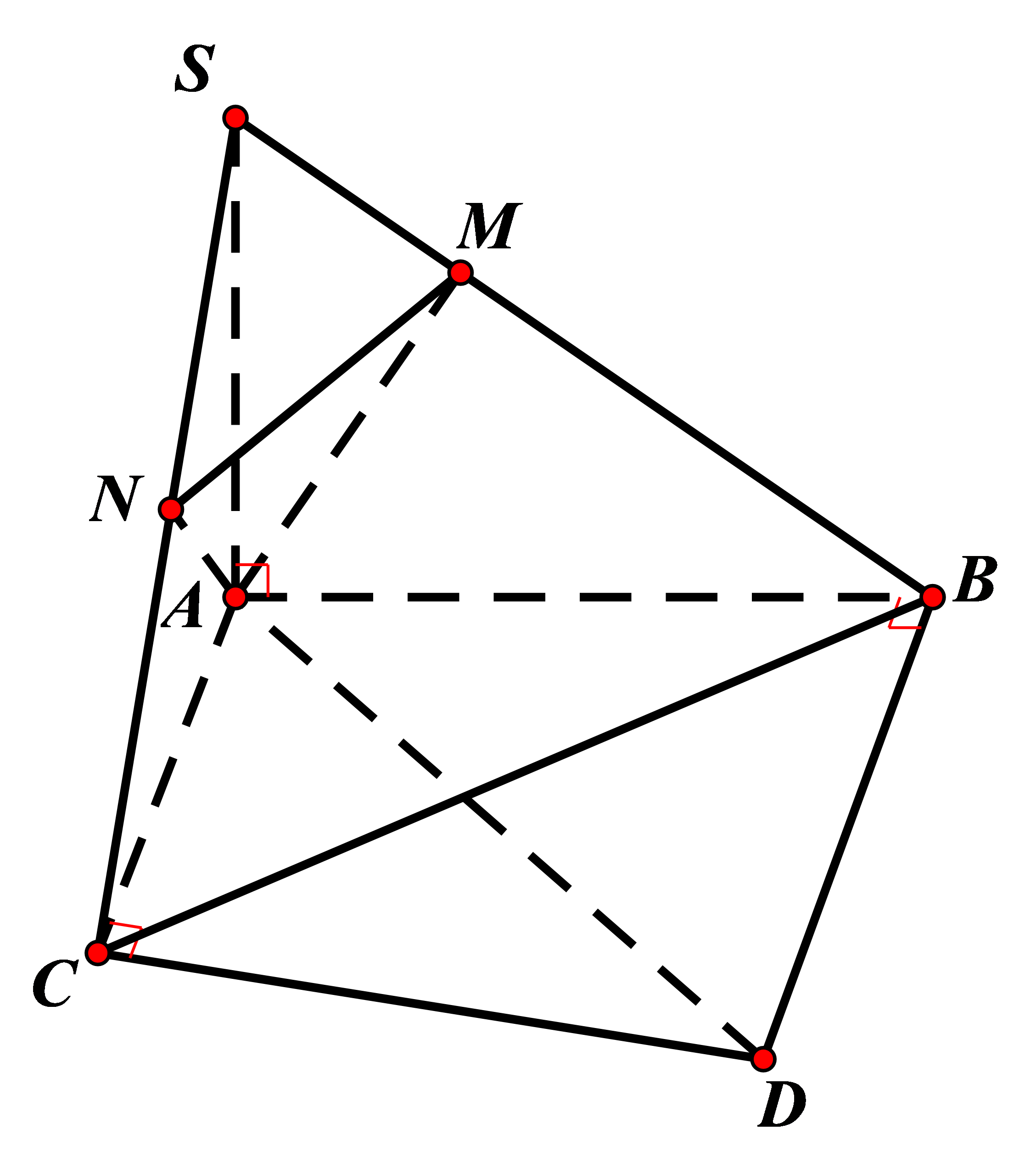
Kẻ đường kính AD của đường tòn ngoại tiếp đáy.
Ta có: \(\left\{ \begin{array}{l}CD \bot AC\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right) \Rightarrow CD \bot AN\)
Mặt khác ta có: \(SC \bot AN\)
\( \Rightarrow AN \bot \left( {SCD} \right) \Rightarrow AN \bot SD\)
Tương tự ta có: \(SD \bot \left( {AMN} \right)\)
Mà \(SA \bot \left( {ABC} \right)\) nên \(\widehat {\left( {\left( {AHK} \right),\left( {ABC} \right)} \right)} = \widehat {\left( {SA,SD} \right)} = \widehat {DSA}\)
Ta có AD là đường kính đường tròn ngoại tiếp tam giác ABC nên ta có:
\(AD = 2R = \dfrac{{BC}}{{\sin A}} = \dfrac{{2a\sqrt 3 }}{3}\)
Xét tam giác SAD vuông tại A ta có:
\(SD = \sqrt {S{A^2} + A{D^2}} = \sqrt {4{a^2} + \dfrac{{4{a^2}}}{3}} = \dfrac{{4a\sqrt 3 }}{3}\)
Vậy \(\sin ASD = \dfrac{{AD}}{{SD}} = \dfrac{1}{2}\)
Hướng dẫn giải:
- Kẻ đường kính AD của đường tòn ngoại tiếp đáy.
- Xác định góc giữa (AMN) và đáy.
- Tính AD và SD.
- Tính góc giữa (AMN) và đáy
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
