Câu hỏi:
2 năm trước
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh bằng $1$, mặt bên $SAB$ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích $V$ của khối cầu ngoại tiếp hình chóp đã cho.
Trả lời bởi giáo viên
Đáp án đúng: b
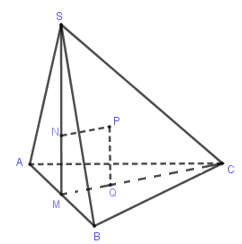
Gọi $M,N,P,Q$ lần lượt là trung điểm $AB$, tâm đường tròn ngoại tiếp $\Delta SAB$, tâm mặt cầu ngoại tiếp hình chóp và tâm đường tròn ngoại tiếp $\Delta ABC \Rightarrow MNPQ$ là hình vuông suy ra
$PN = MQ = \dfrac{1}{3}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{6};NB = \dfrac{2}{3}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{3}$
Bán kính mặt cầu ngoại tiếp chóp là $R = PB = \sqrt {P{N^2} + N{B^2}} = \dfrac{{\sqrt {15} }}{6}$
Thể tích $V = \dfrac{4}{3}\pi {R^3} = \dfrac{{5\sqrt {15} \pi }}{{54}}$
Hướng dẫn giải:
- Xác định tâm đáy và trục tam giác đáy \(ABC\).
- Xác định trục tam giác \(SAB\): là đường thẳng vuông góc với mặt phẳng \(\left( {SAB} \right)\) tại tâm của tam giác.
- Giao điểm của hai đường thẳng trên là tâm mặt cầu ngoại tiếp hình chóp.
Câu hỏi khác
- Đề thi kiểm tra 1 tiết chương 6: Mặt nón, mặt trụ, mặt cầu - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 6: Mặt nón, trụ, cầu - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 6: Mặt nón, mặt trụ, mặt cầu - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 6: Mặt nón, trụ, cầu - Đề số 3 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 6: Mặt nón, trụ, cầu - Đề số 2 Toán 12 có lời giải chi tiết
