Câu hỏi:
2 năm trước
Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại \(B\), cạnh bên S A vuông góc với đáy và \(SA = 2a,AB = BC = a\). Gọi \(M\) là điểm thuộc AB sao cho \(AM = \dfrac{{2a}}{3}\). Tính khoảng cách \(d\) từ điểm \(S\) đến đường thẳng CM.
Trả lời bởi giáo viên
Đáp án đúng: c
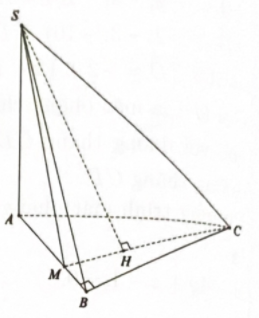
Bước 1: Tính $CM, SM, SC$
$MB=AB-AM=\dfrac{a}{3}$
$AC=AB\sqrt{2}=a\sqrt{2}$
Ta có:
\(CM =\sqrt {{BC^2} + MB^2}= \sqrt {{a^2} + \dfrac{{{a^2}}}{9}} \)\(= \dfrac{{a\sqrt {10} }}{3}\)
\(SM =\sqrt {SA^2 + AM^2} = \sqrt {4{a^2} + \dfrac{{4{a^2}}}{9}} \)\(= \dfrac{{2a\sqrt {10} }}{3}\)
\(SC =\sqrt{SA^2+AC^2}= a\sqrt 6 \)
Bước 2: Đặt \(p = \dfrac{{SM + MC + SC}}{2}\). Tính SH thông qua tính diện tích tam giác SMC.
Đặt \(p = \dfrac{{SM + MC + SC}}{2}\). Diện tích tam giác SMC là
\({S_{\Delta SMC}}\)\( = \sqrt {p(p - SM)(p - CM)(p - SC)} \)\( = \dfrac{{{a^2}\sqrt {11} }}{3}\)
Suy ra khoảng cách từ \(S\) đến $C M$ là
\(d=SH = \dfrac{{2{S_{\Delta SMC}}}}{{CM}} = \dfrac{{a\sqrt {110} }}{5}.\)
Hướng dẫn giải:
Bước 1: Tính CM, SM, SC
Bước 2: Đặt \(p = \dfrac{{SM + MC + SC}}{2}\). Tính SH thông qua tính diện tích tam giác SMC.
