Câu hỏi:
2 năm trước
Cho hình chóp \(S.\,ABC\) có \(AB = AC = 4,\,BC = 2,\,SA = 4\sqrt 3 \), \(\widehat {SAB} = \widehat {SAC} = 30^0\). Tính thể tích khối chóp \(S.\,ABC.\)
Trả lời bởi giáo viên
Đáp án đúng: c
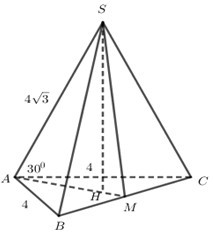
Dễ thấy \(\Delta SAB = \Delta SAC\left( {c.g.c} \right)\) nên \(SB = SC\) hay tam giác \(\Delta SBC\) cân.
Gọi \(M\) là trung điểm \(BC\) ta có: \(AM \bot BC,SM \bot BC \Rightarrow BC \bot \left( {SAM} \right)\).
Gọi \(H\) là hình chiếu của \(S\) trên \(AM\) thì \(SH \bot AM,SH \bot BC\) nên \(SH\) là đường cao của hình chóp.
Xét tam giác \(SAB\) có: \(S{B^2} = S{A^2} + A{B^2} - 2SA.AB\cos {30^0} = 16 \Rightarrow SB = 4 \Rightarrow SC = 4\).
Do đó \(S{M^2} = \dfrac{{S{B^2} + S{C^2}}}{2} - \dfrac{{B{C^2}}}{4} = 15 \Rightarrow SM = \sqrt {15} \).
Tam giác \(ABC\) có \(A{M^2} = \dfrac{{A{B^2} + A{C^2}}}{2} - \dfrac{{B{C^2}}}{4} = 15 \Rightarrow AM = \sqrt {15} \).
Khi đó \({S_{SAM}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = 6\).
Do đó: \(SH = \dfrac{{2{S_{SAM}}}}{{AM}} = \dfrac{{2.6}}{{\sqrt {15} }} = \dfrac{{4\sqrt {15} }}{5}\).
\({V_{S.ABC}} = \dfrac{1}{3}{S_{ABC}}.SH = \dfrac{1}{3}.\dfrac{1}{2}AM.BC.SH = \dfrac{1}{6}.\sqrt {15} .2.\dfrac{{4\sqrt {15} }}{5} = 4\).
Hướng dẫn giải:
- Gọi \(M\) là trung điểm của \(BC\), dựng chiều cao hình chóp.
- Tính diện tích đáy và chiều cao suy ra thể tích \(V = \dfrac{1}{3}Sh\).
