Câu hỏi:
2 năm trước
Cho hình chóp đều $S.ABC$. Mặt phẳng $\left( \alpha \right)$ qua $A$, song song với $BC$ và vuông góc với mặt phẳng $\left( {SBC} \right)$. Thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp đã cho là:
Trả lời bởi giáo viên
Đáp án đúng: b
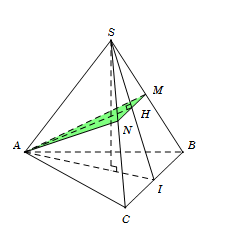
Gọi $I$ là trung điểm $BC$.
Trong tam giác $SAI$ kẻ $AH \bot SI$ $\left( {H \in SI} \right)$.
Trong tam giác $SBC$, qua $H$ kẻ đường song song với $BC$, cắt $SC$ ở $M$, cắt $SB$ ở $N$.
Qua cách dựng ta có $BC\parallel \left( {AMN} \right).$ \(\left( 1 \right)\)
Và $\left\{ \begin{array}{l}SI \bot AH\\SI \bot MN{\rm{ }}\left( {{\rm{do }}SI \bot BC} \right)\end{array} \right. \Rightarrow SI \bot \left( {AMN} \right) \Rightarrow \left( {SBC} \right) \bot \left( {AMN} \right).$
Từ $\left( 1 \right)$ và $\left( 2 \right)$, suy ra thiết diện cần tìm là tam giác $AMN$.
Dễ thấy $H$ là trung điểm của $MN$ mà $AH \bot \left( {SBC} \right)$ suy ra $AH \bot MN$. Tam giác $AMN$ có đường cao $AH$ vừa là trung tuyến nên nó là tam giác cân đỉnh $A$.
