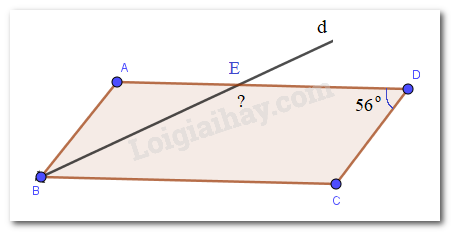
Cho hình bình hành ABCD có \(\widehat D = 56^\circ \). Tia Bd là tia phân giác của \(\widehat {ABC}\), cắt AD tại E. Tính số đo góc BED?
Trả lời bởi giáo viên
Vì ABCD là hình bình hành nên \(\widehat {ABC} = \widehat {ADC}\)( tính chất hình bình hành), mà \(\widehat {ADC} = 56^\circ \Rightarrow \widehat {ABC} = 56^\circ \)
Vì Bd là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {ABE} = \widehat {CBE} = \frac{1}{2}.\widehat {ABC} = \frac{1}{2}.56^\circ = 28^\circ \)
Vì ABCD là hình bình hành nên AD // BC ( tính chất hình bình hành)
\( \Rightarrow \widehat {AEB} = \widehat {CBE}\) ( 2 góc so le trong)
\( \Rightarrow \widehat {AEB} = 28^\circ \)
Ta có: \(\widehat {AEB} + \widehat {BED} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 28^\circ + \widehat {BED} = 180^\circ \\ \Rightarrow \widehat {BED} = 180^\circ - 28^\circ = 152^\circ \end{array}\)
Hướng dẫn giải:
Bước 1: Sử dụng tính chất hình bình hành, suy ra số đo góc ABC.
Bước 2: Sử dụng tính chất tia phân giác của một góc suy ra số đo góc CBE.
Bước 3: Sử dụng tính chất song song , suy ra góc AEB.
Bước 4: Sử dụng tính chất hai góc kề bù suy ra góc BED.