Câu hỏi:
2 năm trước
Cho hệ \(\left\{ \begin{array}{l}2x + 3y < 5\,\,\,(1)\\x + \dfrac{3}{2}y < 5\,\,\,(2)\end{array} \right.\). Gọi \({S_1}\) là tập nghiệm của bất phương trình (1), \({S_2}\) là tập nghiệm của bất phương trình (2) và \(S\) là tập nghiệm của hệ thì
Trả lời bởi giáo viên
Đáp án đúng: a
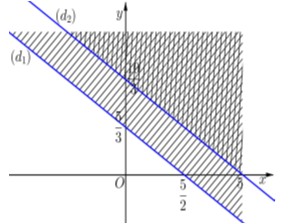
Trước hết, ta vẽ hai đường thẳng:
\(\left( {{d_1}} \right):2x + 3y = 5\)
\(\left( {{d_2}} \right):x + \dfrac{3}{2}y = 5\)
Ta thấy \(\left( {0\,\,;\,\,0} \right)\) là nghiệm của cả hai bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả hai miền nghiệm của hai bất phương trình. Say khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ.
Hướng dẫn giải:
- Biểu diễn miền nghiệm của từng bất phương trình trên mặt phẳng tọa độ.
- Xét tính đúng, sai của từng đáp án.
Câu hỏi khác
- Bài tập bất phương trình và hệ bất phương trình bậc nhất hai ẩn toán 10 có lời giải
- Bài tập bất phương trình và hệ bất phương trình bậc nhất một ẩn toán 10 có lời giải
- Bài tập bất đẳng thức toán 10 có lời giải
- Bài tập dấu của nhị thức bậc nhất toán 10 có lời giải
- Bài tập đại cương về bất phương trình toán 10 có lời giải
