Cho hàm số \(y = \dfrac{x}{{1 - x}}\,\,\left( C \right)\) và điểm \(A\left( { - 1;1} \right)\). Tìm \(m\) để đường thẳng \(d:\,\,y = mx - m - 1\) cắt \(\left( C \right)\) tại 2 điểm phân biệt \(M,\,\,N\) sao cho \(A{M^2} + A{N^2}\) đạt giá trị nhỏ nhất.

Xét phương trình hoành độ giao điểm:.

\(\begin{array}{l}\,\,\,\,\,\,\dfrac{x}{{1 - x}} = mx - m - 1\,\,\left( {x \ne 1} \right)\\ \Leftrightarrow x = \left( {mx - m - 1} \right)\left( {1 - x} \right)\\ \Leftrightarrow x = mx - m - 1 - m{x^2} + mx + x\\ \Leftrightarrow m{x^2} - 2mx + m + 1 = 0\,\,\,\left( * \right)\end{array}\)

Để đường thẳng \(d:\,\,y = mx - m - 1\) cắt \(\left( C \right)\) tại 2 điểm phân biệt \(M,\,\,N\) thì phương trình (*) phải có 2 nghiệm phân biệt khác \(1\) \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {m^2} - m\left( {m + 1} \right) > 0\\m - 2m + m + 1 \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l} - m > 0\\1 \ne 0\end{array} \right. \Leftrightarrow m < 0\).

Khi đó hoành độ của hai điểm \(M,\,\,N\) là nghiệm của phương trình (*), áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_M} + {x_N} = 2\\{x_M}.{x_N} = \dfrac{{m + 1}}{m}\end{array} \right.\).

Ta có: \(\left\{ \begin{array}{l}{y_M} = m{x_M} - m - 1\\{y_N} = m{x_N} - m - 1\end{array} \right.\) \( \Rightarrow {y_M} + {y_N} = \left( {{x_M} + {x_N}} \right) - 2m - 2 =  - 2\).

Gọi \(I\) là trung điểm của \(MN\), ta có \(I\left( {1; - 1} \right)\) \( \Rightarrow A{I^2} = {2^2} + {\left( { - 2} \right)^2} = 8\).

\(\begin{array}{l}M{N^2} = {\left( {{x_M} - {x_N}} \right)^2} + {\left( {{y_M} - {y_N}} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = {\left( {{x_M} - {x_N}} \right)^2} + {\left( {m{x_M} - m - 1 - m{x_N} + m + 1} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = {\left( {{x_M} - {x_N}} \right)^2} + {m^2}{\left( {{x_M} - {x_N}} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = \left( {1 + {m^2}} \right){\left( {{x_M} - {x_N}} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = \left( {1 + {m^2}} \right)\left[ {{{\left( {{x_M} + {x_N}} \right)}^2} - 4{x_M}{x_N}} \right]\\\,\,\,\,\,\,\,\,\,\,\,\, = \left( {1 + {m^2}} \right)\left[ {4 - 4\dfrac{{m + 1}}{m}} \right]\\\,\,\,\,\,\,\,\,\,\,\,\, =  - 4\dfrac{{1 + {m^2}}}{m}\end{array}\)

Do \(M{N^2} > 0\) nên \(m < 0\).

Đặt \(T = A{M^2} + A{N^2}\)

Ta có:

\(\begin{array}{l}A{I^2} = \dfrac{{A{M^2} + A{N^2}}}{2} - \dfrac{{M{N^2}}}{4}\\ \Rightarrow 4A{I^2} = 2T - M{N^2}\\ \Leftrightarrow T = \dfrac{{4A{I^2} + M{N^2}}}{2} \Leftrightarrow T = \dfrac{{4.8 - 4\dfrac{{1 + {m^2}}}{m}}}{2}\\ \Leftrightarrow T = 16 - 2\dfrac{{1 + {m^2}}}{m} \Leftrightarrow T = \dfrac{{ - 2{m^2} + 16m - 2}}{m}\end{array}\)

Ta có:

\(\begin{array}{l}T' = \dfrac{{\left( { - 4m + 16} \right)m - \left( { - 2{m^2} + 16m - 2} \right)}}{{{m^2}}}\\T' = \dfrac{{ - 4{m^2} + 16m + 2{m^2} - 16m + 2}}{{{m^2}}}\\T' = \dfrac{{ - 2{m^2} + 2}}{{{m^2}}} = 0 \Leftrightarrow m =  \pm 1\end{array}\)

BBT:

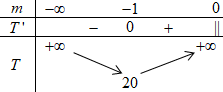
Từ BBT ta thấy \(\min T = 20 \Leftrightarrow m =  - 1\) .