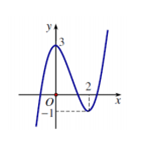
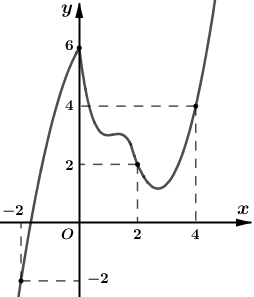
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ. Đặt \(g\left( x \right) = 2f\left( x \right) - {x^2}\). Khi đó giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { - 2;4} \right]\) là:
Trả lời bởi giáo viên
Ta có \(g\left( x \right) = 2f\left( x \right) - {x^2}\) \( \Rightarrow g'\left( x \right) = 2f'\left( x \right) - 2x\)
Cho \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = x\,\,\,\left( 1 \right)\).
Nghiệm của phương trình (1) là hoành độ giao điểm của hai đồ thị hàm số \(y = f'\left( x \right);\,\,y = x.\)
Vẽ đường thẳng \(y = x\) và đồ thị hàm số \(y = f'\left( x \right)\) trên cùng hệ trục tọa độ:
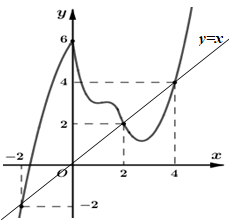
Dựa vào đồ thị ta thấy đồ thị hai hàm số \(y = f'\left( x \right);\,\,y = x\) cắt nhau tại 3 điểm có hoành độ là \( - 2;2;4.\)
\( \Rightarrow g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 2\\x = 4\end{array} \right.\)
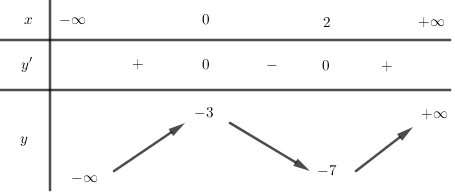
Bảng biến thiên đồ thị hàm số \(y = g\left( x \right)\):
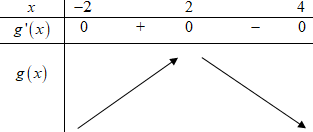
Dựa vào bảng biến thiên ta thấy giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { - 2;4} \right]\) là \(g\left( 2 \right)\).
Hướng dẫn giải:
- Tính đạo hàm của hàm số \(g\left( x \right)\). Xác định các nghiệm của phương trình \(g'\left( x \right) = 0\).
- Xét dấu \(g'\left( x \right)\) thông qua \(f'\left( x \right)\).
- Lập bảng biến thiên của \(g\left( x \right)\) rồi kết luận giá trị lớn nhất của hàm số trên \(\left[ { - 2;4} \right]\).