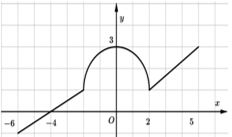
Cho hàm số \(y=f(x)\) liên tục trên đoạn \(\left[ -6;5 \right]\), có đồ thị gồm hai đoạn thẳng và nửa đường tròn như hình vẽ. Tính giá trị \(I=\int\limits_{-6}^{5}{\left[ f(x)+2 \right]dx}\).

\(y=f(x)=\left\{ \begin{align}  \frac{x+4}{2},\,\,x<-2 \\  \sqrt{4-{{x}^{2}}}+1,\,\,-2\le x\le 2 \\  \frac{2x-1}{3},\,\,x>2 \\ \end{align} \right.\,\,\)

\(\begin{align}  I=\int\limits_{-6}^{5}{\left[ f(x)+2 \right]dx}=\int\limits_{-6}^{5}{f(x)dx}+\int\limits_{-6}^{5}{2dx}=\int\limits_{-6}^{-2}{\frac{x+4}{2}dx}+\int\limits_{-2}^{2}{\left( \sqrt{4-{{x}^{2}}}+1 \right)dx}+\int\limits_{2}^{5}{\frac{2x-1}{3}dx}+\int\limits_{-6}^{5}{2dx} \\  =\int\limits_{-6}^{-2}{\frac{x+4}{2}dx}+\int\limits_{-2}^{2}{\sqrt{4-{{x}^{2}}}dx}+\int\limits_{-2}^{2}{dx}+\int\limits_{2}^{5}{\frac{2x-1}{3}dx}+\int\limits_{-6}^{5}{2dx} \\  =0+{{I}_{1}}+4+6+22={{I}_{1}}+32 \\ \end{align}\)

Trong đó \({{I}_{1}}=\int\limits_{-2}^{2}{\sqrt{4-{{x}^{2}}}dx}\), đặt \(x=2\sin t\Rightarrow dx=2\cos tdt\), đổi cận \(x=-2\to t=-\frac{\pi }{2};\,\,x=2\to t=\frac{\pi }{2}\)

 \(\Rightarrow {{I}_{1}}=\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\sqrt{4-4{{\sin }^{2}}t}.2\cos tdt}=4\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{{{\cos }^{2}}tdt}=2\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\left( \cos 2t+1 \right)dt}=\left. \left( \sin 2t+2t \right) \right|_{-\frac{\pi }{2}}^{\frac{\pi }{2}}=2\pi \)

 \(\Rightarrow I=2\pi +32\).