Câu hỏi:
2 năm trước
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a.\) Khoảng cách giữa hai mặt phẳng \((ACD')\) và \((BA'C')\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
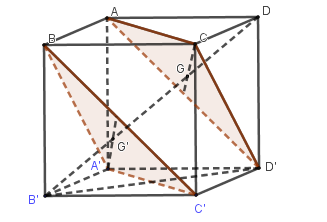
Gọi \(G,G'\) là trọng tâm các tam giác \(ACD',BA'C'\).
Khi đó \(DG \bot \left( {ACD'} \right),B'G' \bot \left( {BA'C'} \right)\) vì các hình chóp \(D.ACD'\) và \(B'.BA'C'\) là hình chóp đều.
Ta có: \(AC \bot \left( {BDD'B'} \right) \Rightarrow AC \bot DB'\)
Lại có \(CD' \bot \left( {ADC'B'} \right) \Rightarrow CD' \bot DB'\).
Do đó \(DB' \bot \left( {ACD'} \right)\).
Tương tự \(DB' \bot \left( {BA'C'} \right)\) nên \(\left( {ACD'} \right)//\left( {BA'C'} \right)\) và \(G,G' \in DB'\).
Do đó \(GG'\) vuông góc cả hai mặt phẳng \(\left( {ACD'} \right),\left( {BA'C'} \right)\).
Vậy khoảng cách giữa hai mặt đó là \(GG'\).
Hướng dẫn giải:
- Gọi \(G,G'\) lần lượt là trọng tâm các tam giác \(ACD'\) và \(BA'C'\).
- Chứng minh khoảng cách giữa hai mặt phẳng \(\left( {ACD'} \right)\) và \(\left( {BA'C'} \right)\) chính là \(GG'\) bằng cách chứng minh \(GG' \bot \left( {ACD'} \right),GG' \bot \left( {BA'C'} \right)\).
Câu hỏi khác
- Đề thi thử THPTQG môn Toán Chuyên ĐH Vinh Nghệ An lần 3 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 1 Toán 12 có lời giải chi tiết
- Đề tập huấn thi THPTQG Sở Giáo Dục và Đào Tạo Bắc Ninh 2019 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 4 Toán 12 có lời giải chi tiết
